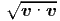
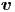 ·
·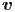

In diesem Abschnitt wollen wir die Wahrscheinlichkeitsdichte für eine bestimmte Geschwindigkeit berechnen. Der Begriff „Geschwindigkeit“ hier ist nicht präzise. Er könnte
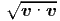
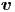 ·
·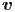
meinen. Je nach gewählter Grösse müssen wir die Geschwindigkeiten anders gewichten. Bei klassischer (nicht- quantenmechanischer) Betrachtungsweise folgt die Wahrscheinlichkeitsdichte f(v) aus der Boltzmannverteilung, wobei die Energie die kinetische Energie ist.
![[ ]
12mv2
f (v) dv = C exp - -kT--- dv](td-2015173x.png) | (2.1) |
C ist ein Normierungsfaktor, der so gewählt werden muss, dass das Integral von f(v) über den ganzen Geschwindigkeitsraum gleich eins ist. Wir betrachten hier den Betrag der Geschwindigkeit, so dass Richtungen beim Mitteln keinen Einfluss haben dürfen.
Je nach der Dimension des Raumes gibt es verschiedene Mittelungsarten:
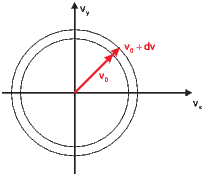
Berechnung der Anzahl Vektoren in einem Geschwindigkeitsintervall
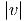 < v0 + dv ist
proportional zu 2πvdv
< v0 + dv ist
proportional zu 2πvdv
Die folgenden Betrachtungen sind alle für drei Dimensionen.
Die Betrachtung der Anzahl möglicher Realisierungen der
Geschwindigkeit v zeigt, dass damit das Maximum der
Boltzmannverteilung bei E = 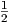 mv2 = 0 zur Position v > 0
verschoben wird.
mv2 = 0 zur Position v > 0
verschoben wird.
Wir verwenden nun den Vorfaktor C′ und erhalten, mit der Integration über die Winkel
![[ ]
′ 2 12mv2--
f (v)dv = C 4πv exp - kT dv](td-2015177x.png) | (2.2) |
f(v) ist normiert, wenn
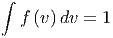 | (2.3) |
ist. Mit der Abkürzung
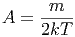 |
bekommen wir
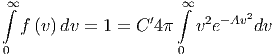 | (2.4) |
Die mathematische Beziehung
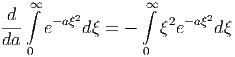 |
hilft, das Integral zu lösen. Wir verwenden weiter Gleichung
(E.2) (∫
0∞e-Av2dv = 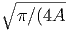 ) aus dem Anhang E.3. Wir
können wie folgt umrechnen
) aus dem Anhang E.3. Wir
können wie folgt umrechnen
| 1 | = C′·4π·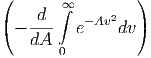 | ||
= C′4π·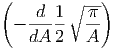 = C′·4π· = C′·4π·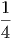 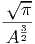 | (2.5) |
Damit wird der Vorfaktor
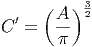 |
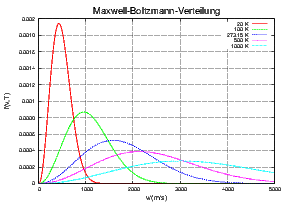
Maxwell-Boltzmann-Verteilung für Wasserstoff H2
Mittelwerte einer Grösse g(v) bezüglich einer Wahrscheinlichkeitsdichte f(v) werden durch
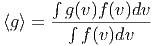 |
berechnet.
Mit dieser Gleichung berechnen wir nun
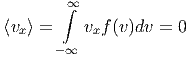 | (2.7) |
da vx eine ungerade Funktion ist und in f(v) nur die gerade Funktion v2 = v x2 + v y2 + v z2 vorkommt.
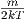 bekommen wir
bekommen wir
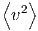 | = ∫
v2f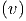 dv dv | = | 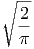 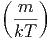 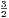 ∫
0∞v4e-Av2
dv
∫
0∞v4e-Av2
dv | ||||
= 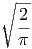 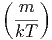 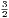
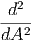 ∫
0∞e-Av2
dv ∫
0∞e-Av2
dv | = | 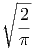 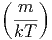 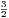
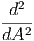 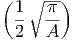 | |||||
= 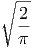 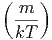 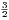 ·
·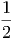 · ·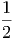 · ·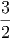 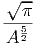 | = | 3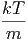 | (2.8) |
d.h. 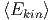 =
= 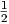 m
m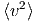 =
= 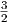 kT folgt aus
Maxwell-Boltzmannverteilung unter der Berücksichtigung
des Phasenraumes.
kT folgt aus
Maxwell-Boltzmannverteilung unter der Berücksichtigung
des Phasenraumes.
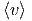 | = ∫
0∞vf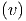 dv = dv = 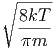 | (2.9) |
Welches ist die häufigste Geschwindigkeit vmax? Die häufigste Geschwindigkeit bei einer nicht-konstanten Wahrscheinlichkeitsdichte ist nicht die mittlere Geschwindigkeit. Wir finden vmax durch Ableiten
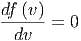 |
Unter Vernachlässigung konstanter Vorfaktoren bekommen wir
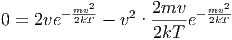 |
Also ist
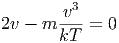 |
Das Maximum der Maxwell-Boltzmann-Verteilung liegt also bei
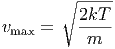 | (2.10) |
Wenn wir die zu vmax gehörige kinetische Energie berechnen, erhalten wir
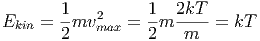 |
Dies ist das Resultat der naiven Mittelung zu Beginn des Kapitels über die Wärmelehre.
Schliesslich betrachten wir die asymptotische Entwicklung von f(v) für v → 0 und v →∞.
Für kleine v lautet die Taylorentwicklung von f(v) um v = 0
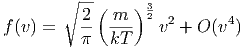 | (2.11) |
Die Notation O(v4) bedeutet, dass der erste nicht verschwindende weitere Summand von der Ordnung v4 ist. Höhere Ordnungen können vorkommen.
Der Anteil der Teilchen mit kinetischen Energien im
Intervall 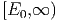 im Vergleich zu allen Teilchen (Intervall
im Vergleich zu allen Teilchen (Intervall
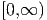 ) ist
) ist
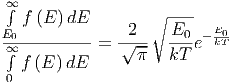 | (2.12) |
 Lizenzinformationen
Lizenzinformationen