Weiter: Abbildungsverzeichnis Oben: Vorlesungsskript PHYS 70357 Elektrizitätslehre Zurück: Übungsdaten Skript: PDF-Datei Übungen: Blätter
![[*]](crossref.gif) , Gleichung (2.75):
, Gleichung (2.75):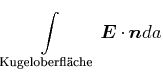 |
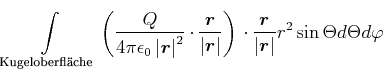 |
||
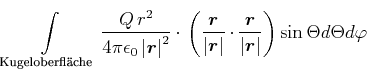 |
|||
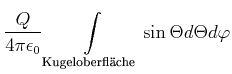 |
|||
![[*]](crossref.gif) , Gleichung (12):
, Gleichung (12):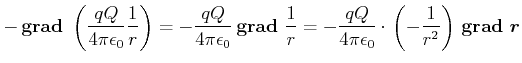 |
|||
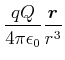 |
![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :
: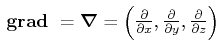
![[*]](crossref.gif) , Gleichung (2.50):
, Gleichung (2.50):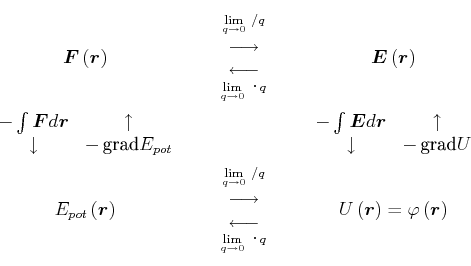 |
![[*]](crossref.gif) , Abschnitt 3.98:
, Abschnitt 3.98:
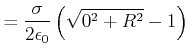 |
||||
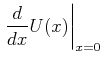 |
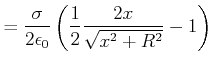 |
|||
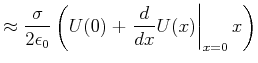 |
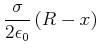 |
Die beiden Grenzfälle zeigen, dass sich die geladene Kreisplatte für ![]() wie eine Punktladung und für
wie eine Punktladung und für
![]() wie eine unendlich ausgedehnte Platte verhält.
wie eine unendlich ausgedehnte Platte verhält.
![[*]](crossref.gif) , Gleichung (2.78):
, Gleichung (2.78):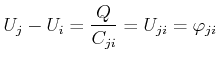 |
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2:![[*]](crossref.gif) , Abschnitt 3.102:
, Abschnitt 3.102:
![\includegraphics[width=0.6\textwidth]{elektrostatik-016}](img392.gif)
|
Auf den positiven Kern wirkt die Kraft
Auf die negative Elektronenwolke wirkt
Die Federkraft wirkt auf die positive Ladung wie
![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :
:
|
Der elektrische Strom |
![[*]](crossref.gif) , Abschnitt 28:
, Abschnitt 28:
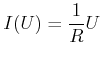 |
![\includegraphics[width=0.7\textwidth]{el-kennlinie-01}](img694.gif)
|
Abbildung G.2 zeigt die Kennlinie eines Widerstandes. Neben Widerständen und Kondensatoren gibt es andere passive und aktive Bauelemente. Die Kennlinien sind meistens nicht linear. Abbildung G.3 zeigt verschiedene Bauelemente.
Diese Bauelemente sind sowohl linear wie nichtlinear. Wenn man die genaue physikalische Funktionsweise eines Bauelementes nicht kennt, dann helfen Kennlinien, trotzdem mit dem Bauelement Schaltungen zu berechnen.
![\includegraphics[width=0.7\textwidth]{el-kennlinie-03}](img696.gif)
|
Abbildung G.4 zeigt wie die Messung geht. Die Spannung ![]() wird über das
Potentiometer
wird über das
Potentiometer ![]() , ein gebräuchlicher Name für einen veränderbaren Widerstand, an den zu testenden
Widerstand
, ein gebräuchlicher Name für einen veränderbaren Widerstand, an den zu testenden
Widerstand ![]() angeschlossen. Mit einem (idealen) Voltmeter wird die Spannung
angeschlossen. Mit einem (idealen) Voltmeter wird die Spannung ![]() am Widerstand
am Widerstand ![]() gemessen. Das ideale Ampèremeter misst den Strom durch
gemessen. Das ideale Ampèremeter misst den Strom durch ![]() durch den Widerstand
durch den Widerstand ![]() . Diese beiden
Grössen werden denn wie in Abbildung G.2 aufgezeichnet.
. Diese beiden
Grössen werden denn wie in Abbildung G.2 aufgezeichnet.
![\includegraphics[width=0.6\textwidth]{el-kennlinie-05}](img700.gif)
|
![\includegraphics[width=0.7\textwidth]{el-kennlinie-04}](img701.gif)
Kennlinie einer Diode vom Typ 1N4148 gemessen mit der Schaltung nach Abbildung
G.5.
|
Als Beispiel eines nichtlinearen Bauelementes zeigt Abbildung G.5 die
Messschaltung und Abbildung G.6 die Kennlinie der Diode 1N4148. Für positive
Spannungen ![]() ist die Diode in Durchlassrichtung gepolt. Deshalb sind die Ströme bei kleinen
Spannungen sehr gross. In der Sperrrichtung Sind die Ströme viel kleiner. Diese können an der
rechten Skala abgelesen werden.
ist die Diode in Durchlassrichtung gepolt. Deshalb sind die Ströme bei kleinen
Spannungen sehr gross. In der Sperrrichtung Sind die Ströme viel kleiner. Diese können an der
rechten Skala abgelesen werden.
![\includegraphics[width=0.7\textwidth]{el-kennlinie-06}](img702.gif)
|
Abbildung G.7 zeigt einen Spannungsteiler bestehend aus den Widerständen ![]() und
und ![]() . Die Spannung an
. Die Spannung an ![]() und die Spannung an
und die Spannung an ![]() sind in Serie. Es muss gelten
sind in Serie. Es muss gelten
Andererseits fliesst der gleiche Strom durch ![]() und
und ![]() und durch den Ersatzwiderstand
und durch den Ersatzwiderstand ![]() . Also
hat man
. Also
hat man
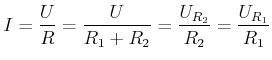 |
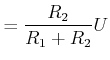 |
|||
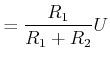 |
![\includegraphics[width=0.7\textwidth]{el-kennlinie-07}](img717.gif)
Gemeinsame Auftragung der Kennlinien zweier in Reihe
geschalteter Widerstände
|
Die beiden Kennlinien in Abbildung G.8 schneiden sich bei
![]() und
und
![]() . Nur an diesem Punkt stimmt an beiden Widerständen die Beziehung zwischen Strom und
Spannung (Ohmsches Gesetz) und gleichzeitig ist die Summer der Spannungsabfälle gleich der
Batteriespannung. Setzt man in Gleichung (3.76) und Gleichung (3.77) die Werte für
. Nur an diesem Punkt stimmt an beiden Widerständen die Beziehung zwischen Strom und
Spannung (Ohmsches Gesetz) und gleichzeitig ist die Summer der Spannungsabfälle gleich der
Batteriespannung. Setzt man in Gleichung (3.76) und Gleichung (3.77) die Werte für ![]() ,
,
![]() und
und ![]() ein, erhält man das gleiche Ergebnis. Das Verfahren zur Bestimmung des Arbeitspunktes
ist unabhängig von der Tatsache, dass Widerstände lineare Bauelemente sind. Es funktioniert auch mit
Dioden und jeglichen anderen nichtlinearen Bauelementen.
ein, erhält man das gleiche Ergebnis. Das Verfahren zur Bestimmung des Arbeitspunktes
ist unabhängig von der Tatsache, dass Widerstände lineare Bauelemente sind. Es funktioniert auch mit
Dioden und jeglichen anderen nichtlinearen Bauelementen.
| Um grafisch die Spannungsabfälle an zwei in Serie geschalteten Bauelementen zu bestimmen, trägt man die Kennlinien einmal mit zunehmender und für das andere Bauelement mit abnehmender Spannung übereinander auf. Der Schnittpunkt ist der gesuchte Arbeitspunkt. Die Spannungen an den zwei Bauelementen können an der entsprechenden Skala direkt abgelesen werden. |
![\includegraphics[width=0.5\textwidth]{el-kennlinie-09}](img721.gif)
|
![\includegraphics[width=0.7\textwidth]{el-kennlinie-08}](img722.gif)
Arbeitspunkt einer Diode vom Typ 1N4148 in Serie mit einem Widerstand
|
Aus der Abbildung G.10 liest man ab, dass am Arbeitspunkt der Schaltung nach
Abbildung G.9 die Spannung
![]() und an dem Widerstand die Spannung
und an dem Widerstand die Spannung
![]() abfällt. Durch beide Bauteile fliesst der Strom
abfällt. Durch beide Bauteile fliesst der Strom ![]() . Das Verfahren nach
Abbildung G.10 ist universell anwendbar.
. Das Verfahren nach
Abbildung G.10 ist universell anwendbar.
Ein Transistor hat drei Anschlüsse, den Emitter (E), den Kollektor (C) und die Basis (B). Im Schaltschema ist der Anschluss mit dem Pfeil der Emitter, derjenige auf der gleichen Seite ohne Pfeile der Kollektor und derjenige auf der anderen Seite die Basis.
![\includegraphics[width=0.3\textwidth]{el-kennlinie-11}](img726.gif)
![\includegraphics[width=0.6\textwidth]{el-kennlinie-10}](img727.gif)
Links: Basis-Emitter-Kennlinie des Transistors BC107, rechts: Kollektor-Kennlinie des
Transistors BC107 mit dem Basisstrom
|
Die Basis-Emitter-Kennlinie in Abbildung G.11 ist die gewöhnliche
Diodenkennlinie. Die rechte Seite von Abbildung G.11 zeigt das
Kollektor-Kennlinienfeld des Transistors. Dieses Kennlinienfeld wird manchmal auch das
Ausgangskennlinienfeld genannt. Beim Ausgangaskennlinienfeld wird der Basisstrom ![]() als Parameter
verwendet. Die Abbildung G.11 zeigt die Kennlinien bei festgehaltenem
Basuisstrom, wobei die Basisströme von
als Parameter
verwendet. Die Abbildung G.11 zeigt die Kennlinien bei festgehaltenem
Basuisstrom, wobei die Basisströme von
![]() bis
bis
![]() in Schritten von
in Schritten von ![]() variieren.
variieren.
Bei vorgegebener Kollektor-Emitter-Spannung ![]() kann man so den Ausgangsstrom am Kollektor bestimmen.
Analog kann bei vorgegebenem Kollektorstrom die Spannung zwischen Emitter und Kollektor als Funktion des
Basisstroms abgelesen werden. Dies ist wichtig, wenn der Transistor als Schalter verwendet werden soll.
kann man so den Ausgangsstrom am Kollektor bestimmen.
Analog kann bei vorgegebenem Kollektorstrom die Spannung zwischen Emitter und Kollektor als Funktion des
Basisstroms abgelesen werden. Dies ist wichtig, wenn der Transistor als Schalter verwendet werden soll.
![\includegraphics[width=0.6\textwidth]{el-kennlinie-13}](img733.gif)
Schaltung zur Messung des Ausgangskennlinie des Transistors BC107 mit einem
Kollektorwiderstand von
|
![\includegraphics[width=0.7\textwidth]{el-kennlinie-12}](img734.gif)
Arbeitskennlinie des Transistors BC107 mit einem Kollektorwiderstand von
|
Die Abbildung G.12 zeigt die Schaltung eines Transistorverstärkers. Der Strom in
die Basis ![]() steuert den Strom im Kollektor
steuert den Strom im Kollektor ![]() .Der Kollektorstrom fliesst durch den Widerstand
.Der Kollektorstrom fliesst durch den Widerstand
![]() . Die Summe der Spannungsabfälle an beiden Bauelementen muss der Batteriespannung
. Die Summe der Spannungsabfälle an beiden Bauelementen muss der Batteriespannung ![]() entsprechen.
Wir können also analog wie bei der Diode vorgehen (siehe Abbildung G.10): Wir
zeichnen die Kennlinie des Widerstandes wie bei der Diode rückläufig ein. Die Schnittpunkte der
Kennlinie des Widerstandes mit den verschiedenen, basisstromabhängigen Ausgangskennlinien des
Transistors sind die Kurve, die die Storm- oder Spannungsverstärkung angibt.
entsprechen.
Wir können also analog wie bei der Diode vorgehen (siehe Abbildung G.10): Wir
zeichnen die Kennlinie des Widerstandes wie bei der Diode rückläufig ein. Die Schnittpunkte der
Kennlinie des Widerstandes mit den verschiedenen, basisstromabhängigen Ausgangskennlinien des
Transistors sind die Kurve, die die Storm- oder Spannungsverstärkung angibt.
![\includegraphics[width=0.7\textwidth]{el-kennlinie-14}](img736.gif)
Verstärkung eines Transistors in
der Emitterschaltung (Der Emitter wird sowohl vom Eingang wie vom Ausgang
verwendet.)
|
Abbildung G.14 zeigt sowohl die Kolektor-Emitterspannung
![]() wie auch
den Kollektorstrom
wie auch
den Kollektorstrom ![]() . Die Verstärkung ist für den Basisstrombereich
. Die Verstärkung ist für den Basisstrombereich
![]() linear. Die Verstärkungswerte sind in Tabelle G.1 angegeben.
linear. Die Verstärkungswerte sind in Tabelle G.1 angegeben.
|
Wenn das Eingangssignal nicht ein Strom, sondern eine Spannung sein soll, muss die Spannung mit einem Widerstand in einen Strom umgewandelt werden.
![\includegraphics[width=0.7\textwidth]{el-kennlinie-15}](img742.gif)
|
Zum Schluss dieses Abschnittes wollen wir die Schaltung nach Abbildung G.15
besprechen. Wir verwenden die Daten aus Abbildungen G.13 und
G.14. Der Widerstand ![]() ist der Arbeitswiderstand
ist der Arbeitswiderstand ![]() aus Abbildung
G.12. Wir hatten immer eine Spannung von
aus Abbildung
G.12. Wir hatten immer eine Spannung von ![]() über dem Arbeitswiderstand
über dem Arbeitswiderstand ![]() (oder
(oder ![]() hier) und dem Transistor. Wir wollen dies beibehalten und gleichzeitig einen
Spannungsabfall von
hier) und dem Transistor. Wir wollen dies beibehalten und gleichzeitig einen
Spannungsabfall von ![]() über
über ![]() haben. Bei unseren vorherigen Berechnungen war
haben. Bei unseren vorherigen Berechnungen war
![]() . Den Arbeitspunkt setzen wir in etwa in die Mitte des linearen Bereiches, bei
. Den Arbeitspunkt setzen wir in etwa in die Mitte des linearen Bereiches, bei
![]() und bei
und bei
![]() . Damit ist
. Damit ist
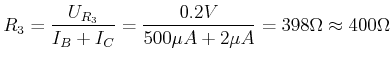
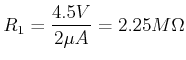
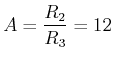
|
Weiterführende Informationen finden Sie im Skript Physikalische Elektronik und Messtechnik
[Mar08].
[Seite: ![[*]](crossref.gif) , Gleichung (30):]
, Gleichung (30):]
![$\displaystyle M\left\langle \vec{v}\right\rangle =\frac{1}{N}\sum\limits_{j=1}^{N}\left[ M\vec{v}_{j}^{\left( k\right) }+q\vec{E}\Delta t_{j}\right]$](img600.gif) |
[Seite: ![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]Wenn der Kondensator von allen Spannungsquellen getrennt ist, bleibt die Ladung auf seinen Platten,
:]Wenn der Kondensator von allen Spannungsquellen getrennt ist, bleibt die Ladung auf seinen Platten, ![]() ,
konstant. Die dielektrische Verschiebung
,
konstant. Die dielektrische Verschiebung ![]() und nicht das elektrische Feld
und nicht das elektrische Feld ![]() bleiben
konstant.
bleiben
konstant.
[Seite: ![[*]](crossref.gif) , Gleichung (30):]
, Gleichung (30):]
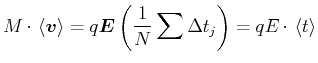 |
![[*]](crossref.gif) , Abbildung 4.19:]
, Abbildung 4.19:]
![\includegraphics[width=0.5\textwidth]{elektrostatik-034}](img646.gif)
|
![[*]](crossref.gif) , Abschnitt 4.1.5:] Wir verwenden die Lorentztransformation der Impulse
, Abschnitt 4.1.5:] Wir verwenden die Lorentztransformation der Impulse 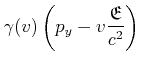 |
|||
![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]wobei
:]wobei ![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]
Bezüglich 0 ist die Situation symmetrisch. Die in der Zeichnung vertikalen Leiterelemente
liefern kollineare sich aufhebende Kräfte. Die horizontalen Segmente ergeben das Drehmoment
:]
Bezüglich 0 ist die Situation symmetrisch. Die in der Zeichnung vertikalen Leiterelemente
liefern kollineare sich aufhebende Kräfte. Die horizontalen Segmente ergeben das Drehmoment
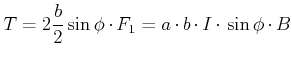 |
![[*]](crossref.gif) , Gleichung (6.79):]
, Gleichung (6.79):]
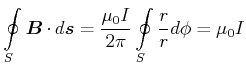 |
![[*]](crossref.gif) , Abschnitt 6.7.2:]Ein zylindrischer Leiter mit dem Radius
, Abschnitt 6.7.2:]Ein zylindrischer Leiter mit dem Radius 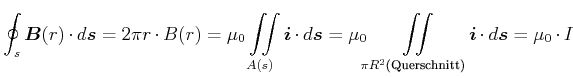
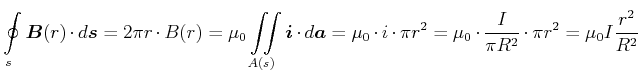
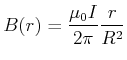
![[*]](crossref.gif) , Abschnitt 13:]Wir definieren eine lineare Stromdichte
, Abschnitt 13:]Wir definieren eine lineare Stromdichte
Wir betrachten weiter die Komponenten ![]() und
und ![]() des Feldes
des Feldes ![]() im Abstand
im Abstand ![]() von der
Platte. Wir werden zwei Symmetrieoperationen an:
von der
Platte. Wir werden zwei Symmetrieoperationen an:
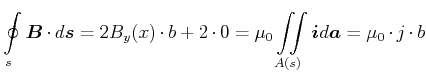
Das Resultat ist unabhängig von ![]() und homogen im Raum. Die Magnetfeldlinien sind parallel zur Platte und
links und rechts antiparallel (siehe Abbildung 3.32, Mitte).
[Seite:
und homogen im Raum. Die Magnetfeldlinien sind parallel zur Platte und
links und rechts antiparallel (siehe Abbildung 3.32, Mitte).
[Seite: ![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]Die potentielle Energie
:]Die potentielle Energie ![]() einer um den Winkel
einer um den Winkel ![]() gegenüber dem Magnetfeld verdrehten
stromdurchflossenen Leiterschlaufe wird berechnet, indem man von
gegenüber dem Magnetfeld verdrehten
stromdurchflossenen Leiterschlaufe wird berechnet, indem man von ![]() ausgeht und die Schlaufe
langsam zum Winkel
ausgeht und die Schlaufe
langsam zum Winkel ![]() dreht. Die Arbeit, um von
dreht. Die Arbeit, um von ![]() nach
nach
![]() zu drehen ist
zu drehen ist
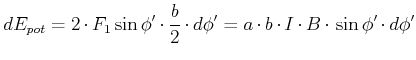 |
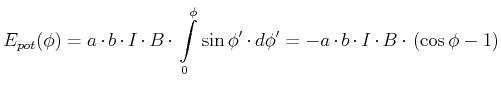 |
![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]In diesem Abschnitt wollen wir die Frage lösen: wie konstruiere ich eine magnetische Induktion
:]In diesem Abschnitt wollen wir die Frage lösen: wie konstruiere ich eine magnetische Induktion
[Seite: ![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]Wir hatten in Abbildung 3.32 gesehen, dass ein homogener Strom in die
:]Wir hatten in Abbildung 3.32 gesehen, dass ein homogener Strom in die ![]() -Richtung homogene
magnetische Induktionen links und rechts erzeugt. Die Magnetfelder haben die Form
-Richtung homogene
magnetische Induktionen links und rechts erzeugt. Die Magnetfelder haben die Form
Für ![]() ist
ist ![]() nicht definiert.
nicht definiert.
![\includegraphics[width=0.7\textwidth]{strom-051}](img1023.gif)
Darstellung von
|
Das zu Gleichung (3.151) gehörige Vektorpotential ist
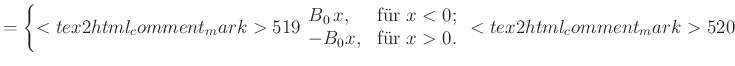 |
||
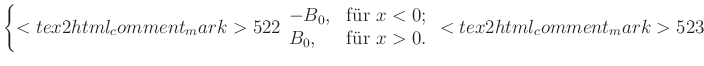 |
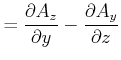 |
|||
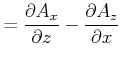 |
||||
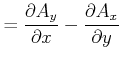 |
0 |
![\includegraphics[width=0.7\textwidth]{strom-050}](img1037.gif)
|
[Seite: ![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]Die Hallspannung für ein einzelnes Teilchen ist unabhängig vom Material. Bei vielen Ladungsträgern muss die
Geschwindigkeit
:]Die Hallspannung für ein einzelnes Teilchen ist unabhängig vom Material. Bei vielen Ladungsträgern muss die
Geschwindigkeit ![]() durch die Driftgeschwindigkeit
durch die Driftgeschwindigkeit
![]() der Ladungsträger ersetzt werden.
der Ladungsträger ersetzt werden.
![]() ist materialabhängig. Strom
ist materialabhängig. Strom ![]() und Driftgeschwindigkeit
und Driftgeschwindigkeit
![]() hängen über
[Seite:
hängen über
[Seite: ![[*]](crossref.gif) , Gleichung (
, Gleichung (![[*]](crossref.gif) ):]
):]
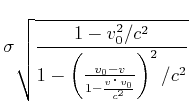 |
|||
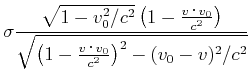 |
|||
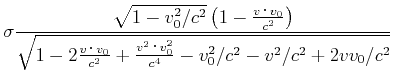 |
|||
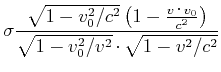 |
|||
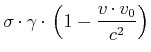 |
![[*]](crossref.gif) , Gleichung (
, Gleichung (![[*]](crossref.gif) ):]
):]
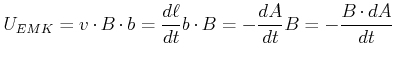 |
![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]Im Vakuum gilt
:]Im Vakuum gilt
Bei einer Bewegung in die
transformiert. |
![\includegraphics[width=0.4\textwidth]{magnetismus-006a}](img1206.gif)
Die magnetische Induktion am Punkt 0 auf der
|
Ausgehend von Gleichung (3.150) schreiben wir für einen Kreisring auf der Position ![]() mit dem
Radius
mit dem
Radius ![]() für
für
![]() .
.
Da ![]() konstant ist, schreiben wir
konstant ist, schreiben wir ![]() und
und ![]() als Funktion des Winkels
als Funktion des Winkels ![]()
Ein Längenelement entlang des Kreisringes ist
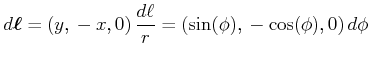
Das Vektorprodukt
![]() ergibt
ergibt
Mit dem Strom pro Windung ![]() wird die magnetische Induktion am Punkte
wird die magnetische Induktion am Punkte
![]()
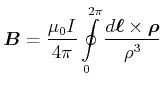 |
Die ![]() - und die
- und die ![]() -Komponenten von
-Komponenten von
![]() enthalten eine Winkelfunktion zur ersten
Potenz und ergeben bei einer Integration von 0 nach
enthalten eine Winkelfunktion zur ersten
Potenz und ergeben bei einer Integration von 0 nach ![]() null. Die
null. Die ![]() -Komponente der magnetischen
Induktion ist
-Komponente der magnetischen
Induktion ist
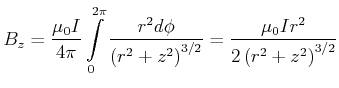 |
Die magnetische Induktion einer unendlich langen Spule bekommt man, indem wir den Strom ![]() durch das Produkt
aus Strom
durch das Produkt
aus Strom ![]() , der Windungszahl pro Länge (Windungsdichte)
, der Windungszahl pro Länge (Windungsdichte) ![]() und dem Längenelement
und dem Längenelement ![]() ersetzen und
integrieren.
ersetzen und
integrieren.
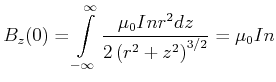 |
Wird die unendlich lange Spule bei ![]() geteilt, tragen beide Spulenhälften gleichviel zur magnetischen
Induktion bei
geteilt, tragen beide Spulenhälften gleichviel zur magnetischen
Induktion bei ![]() bei. Wird nun eine Hälfte entfernt, so ist die magnetische Induktion auf der Spulenachse
bei. Wird nun eine Hälfte entfernt, so ist die magnetische Induktion auf der Spulenachse
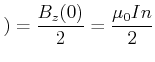 |
Endlich lange Spulen der Länge
![]() verhalten sich wie unendlich lange Spulen. Wenn sich auf der Länge
verhalten sich wie unendlich lange Spulen. Wenn sich auf der Länge
![]()
![]() Windungen befinden, haben wir
Windungen befinden, haben wir
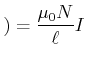 |
[Seite: ![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]Um die Grössenordnung des Wirbelstromes abzuschätzen betrachten wir lokal ein Stück Metall das mit der
Geschwindigkeit
:]Um die Grössenordnung des Wirbelstromes abzuschätzen betrachten wir lokal ein Stück Metall das mit der
Geschwindigkeit ![]() durch eine magnetische Induktion in die
durch eine magnetische Induktion in die ![]() - Richtung,
- Richtung, ![]() , gezogen wird. Wir
betrachten die Felder im Ruhesystem der Platte. Aus den Lorentz-Transformationen erhalten wir
, gezogen wird. Wir
betrachten die Felder im Ruhesystem der Platte. Aus den Lorentz-Transformationen erhalten wir
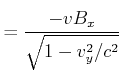 |
|||||
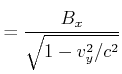 |
da
![]() ist. Lokal gilt der Zusammenhang
ist. Lokal gilt der Zusammenhang
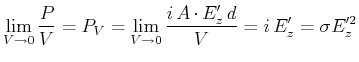 |
Die Berechnung wurde anhand eines unendlich ausgedehnten Leiters in einem Magnetfeld gemacht. Endliche Leiter und endliche Magnetfelder bewirken, dass der Effekt nur an den Grenzen vorhanden ist.
![\includegraphics[width=0.7\textwidth]{magnetismus-005a}](img1205.gif)
Bewegung eines Leiters aus einem Magnetfeld.
|
Im Ruhesystem des Leiters bewirkt das elektrische Feld eine Bewegung der Ladungsträger an die Seiten des
Leiters (analog wie beim Halleffekt). Dadurch wird ein Gegenfeld aufgebaut, bis die Bewegung der Ladungsträger
zum Erliegen kommt (Siehe Abbildung 4.7, linke Seite). Wenn der Leiter den Bereich des
Magnetfeldes verlässt (wir nehmen eine scharfe Grenze an, dann gleichen sich die Ladungen aus. Die Ströme
erzeugen wegen der endlichen Leitfähigkeit ![]() eine Wärmeleistung, das heisst es gibt eine Gegenkraft.
Kondensatoren werden exponentiell entladen, so dass die Wirkung des ändernden Feldes lokal begrenzt ist. Auf
der anderen Seite des Magnetfeldes tauchen die gleichen Effekte auf, aber beim Laden des Kondensators. Auch
dort nimmt der Strom exponentiell ab beim Entfernen von der Grenze. Warum heisst es dann doch Wirbelströme?
Wir haben einen Stromkreis, bei dem die magnetische Induktion die elektromotorische Kraft bewirkt (wie beim
van de Graaff-Generator). Während im Ruhesystem des Leiters die Effekte durch das elektrische Feld erklärt
werden, müssen sie im Laborsystem mit Flussänderung und magnetischer Induktion beschrieben werden.
eine Wärmeleistung, das heisst es gibt eine Gegenkraft.
Kondensatoren werden exponentiell entladen, so dass die Wirkung des ändernden Feldes lokal begrenzt ist. Auf
der anderen Seite des Magnetfeldes tauchen die gleichen Effekte auf, aber beim Laden des Kondensators. Auch
dort nimmt der Strom exponentiell ab beim Entfernen von der Grenze. Warum heisst es dann doch Wirbelströme?
Wir haben einen Stromkreis, bei dem die magnetische Induktion die elektromotorische Kraft bewirkt (wie beim
van de Graaff-Generator). Während im Ruhesystem des Leiters die Effekte durch das elektrische Feld erklärt
werden, müssen sie im Laborsystem mit Flussänderung und magnetischer Induktion beschrieben werden.
In Transformatoren ist die magnetische Induktion parallel zum Eisen, die Wirbelströme transversal dazu. Die Wirbelströme können vermindert werden, indem das Metall geschlitzt wird oder in Lagen mit Isolatoren dazwischen gebündelt wird.
![[*]](crossref.gif) , Gleichung (
, Gleichung (![[*]](crossref.gif) ):]
):]
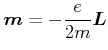 |
![[*]](crossref.gif) , Gleichung (
, Gleichung (![[*]](crossref.gif) ):]
):]
![[*]](crossref.gif) , Gleichung (
, Gleichung (![[*]](crossref.gif) ):]
):]
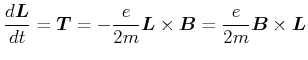 |
![[*]](crossref.gif) , Gleichung (
, Gleichung (![[*]](crossref.gif) ):]
):]
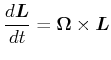 |
![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]Das magnetische Moment des Elektrons ist dann
:]Das magnetische Moment des Elektrons ist dann
![[*]](crossref.gif) , Abschnitt
, Abschnitt ![[*]](crossref.gif) :]Sei
:]Sei ![[*]](crossref.gif) , Gleichung (6.66):]
, Gleichung (6.66):]
![[*]](crossref.gif) , Gleichung (6.68):]
, Gleichung (6.68):]
![[*]](crossref.gif) , Gleichung (6.55):]
, Gleichung (6.55):]
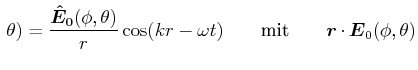 |