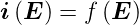

(Siehe Leisi, Klassische Physik II [Lei98, pp. 71]) (Siehe Tipler, Physik [TM04, pp. 751])
| Versuch zur Vorlesung: | |
| Strom-Spannungs-Kennlinie (Versuchskarte EM-83) | |
Allgemein gilt für einen Leiter, dass
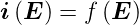 | (3.1) |
eine beliebige Funktion des angelegten Feldes 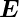 ist. Im
linearen Fall
ist. Im
linearen Fall
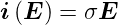 | (3.2) |
spricht man von einem Ohmschen Leiter.
| Versuch zur Vorlesung: | |
| Ohmscher Leiter (Versuchskarte EM-117) | |
σ ist die Leitfähigkeit. Ihre Einheit ist
![[σ ] = A--· m--= -A---= --1-
m2 V Vm Ωm](el-2017367x.png)
Das Gesetz nach Gleichung (3.2) heisst das lokale Ohmsche Gesetz. Für homogene Medien ist σ eine Zahl. Für inhomogene Medien wie Graphit ist σ ein Tensor. Indem wir die differentielle Form des Ohmschen Gesetzes integrieren, erhalten wir
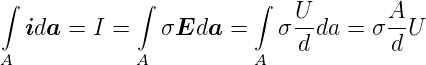 | (3.3) |
Dabei haben wir angenommen, dass 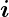 und σ konstant
über A sind. Das integrale Ohmsche Gesetz kann auch
als
und σ konstant
über A sind. Das integrale Ohmsche Gesetz kann auch
als
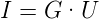 | (3.4) |
geschrieben werden. G ist der Leitwert. Die Einheit ist
![--A-- m2- A--
[G ] = Siemens = S = Vm · m = V](el-2017371x.png)
Bekannter ist die Form
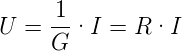 | (3.5) |
R = 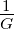 ist der Widerstand. Seine Einheit ist das Ohm
ist der Widerstand. Seine Einheit ist das Ohm
![[R ] = Ω = 1-= V-= W--
S A A2](el-2017374x.png)
Die zu R gehörende mikroskopische Grösse ist der spezifische Widerstand
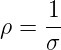 | (3.6) |
Die Einheiten sind
![-Vm-- -m-
[ρ] = A = Ωm = S](el-2017376x.png)
sowie
![[σ] = -A--= S- = -1--
Vm m Ωm](el-2017377x.png)
Wir betrachten die Bewegung von Ionen  in
einer Umgebung von nicht ionisierten Molekülen
in
einer Umgebung von nicht ionisierten Molekülen
__________________________________________________________________________
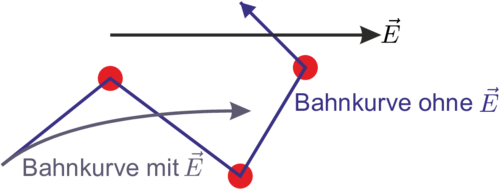
Bahnkurven ohne und mit elektrischem Feld.
_____________________________________________________________________
Die Masse eines Ions sei M, ihre Ladung q und die Gesamtzahl im betrachteten Volumenelement N
Die Newtonsche Bewegungsgleichung lautet
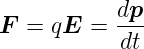 | (3.7) |
oder
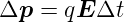 | (3.8) |
wobei Δt die freie Flugzeit ist.
Der mittlere Impuls eines Ions ist
![-1-N∑ [ (k) ]
M ⟨v⟩ = N M v j + qE Δtj
j=1](el-2017381x.png) | (3.9) |
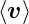 ist die mittlere Driftgeschwindigkeit,
ist die mittlere Driftgeschwindigkeit, 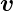 j
j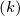 die
Geschwindigkeit nach dem letzten Stoss.
die
Geschwindigkeit nach dem letzten Stoss.
Sind die Geschwindigkeiten 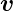 j
j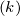 isotrop verteilt, mittelt
sich der erste Summand zu null. Unter dieser Annahme
ist
isotrop verteilt, mittelt
sich der erste Summand zu null. Unter dieser Annahme
ist
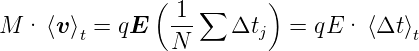 | (3.10) |
wobei 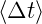 t = τ die mittlere Zeit zwischen den Zusammenstössen
ist. Mit
t = τ die mittlere Zeit zwischen den Zusammenstössen
ist. Mit 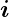 = nq
= nq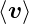 t bekommen wir
t bekommen wir
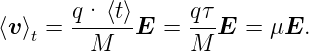 | (3.11) |
Hier ist μ = 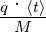 =
= 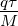 die Beweglichkeit der
Ladungsträger mit der Ladung q und der Masse M. Die
Einheit der Beweglichkeit ist
die Beweglichkeit der
Ladungsträger mit der Ladung q und der Masse M. Die
Einheit der Beweglichkeit ist
![2
[μ ] = m- = Cs-
Vs kg](el-2017394x.png) |
Weiter ist
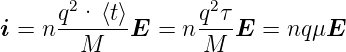 | (3.12) |
Dabei ist n die Dichte der Ladungsträger.
Somit ist bei einer Mischung verschiedener Ladungsträger
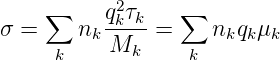 | (3.13) |
Von Gleichung (3.11) an wurde τ = 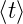 gesetzt.
gesetzt.
Das Ohmsche Gesetz gilt, wenn τk, nk und μk unabhängig
vom elektrischen Feld 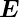 sind.
sind.
Beispiel: Metall
Wir nehmen an, dass me « mKern ist. Dann sind die
Geschwindigkeiten nach dem Stossen isotrop verteilt. Die
mittlere Geschwindigkeit der Elektronen ist 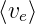 = 105m∕s
(kinetische Gastheorie). Mit
= 105m∕s
(kinetische Gastheorie). Mit
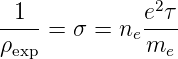 | (3.14) |
bekommen wir
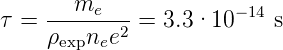 | (3.15) |
(mit ρexp = 4.3 × 10−8 Ωm und n e = 2.5·1028/m3 für Na-Metall)
Die mittlere freie Weglänge ist dann
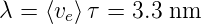 | (3.16) |
im Widerspruch zum Ionenabstand von 0.1 nm 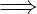 Lösung: Quantenmechanik
Lösung: Quantenmechanik
| Folien zur Vorlesung vom 14. 05. 2009: PDF | |
| Aufgabenblatt 05 für das Seminar vom 20. 05. 2009 (Ausgabedatum 14. 05. 2009): (HTML oder PDF) | |
| Versuch zur Vorlesung: | |
| Leitfähigkeit (Versuchskarte EM-172) | |
| Versuch zur Vorlesung: | |
| Temperaturabhängigkeit der Leitfähigkeit (Versuchskarte TH-122) | |
Bei einem homogenen Ohmschen Leiter mit einer stationären Stromverteilung ist ρel = 0 im Inneren. Dies folgt aus
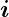
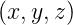 = σ
= σ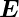
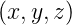
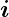 = 0, also
div
= 0, also
div 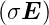 = 0
= 0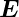 = 0
= 0
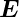 =
= 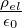
Aus der Eigenschaft
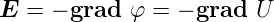 | (3.17) |
erhalten wir im Inneren eines Leiters
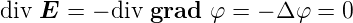 | (3.18) |
Dies bedeutet, dass φ im Inneren eines homogenen Ohmschen Leiters das Potential eines Potentialfeldes ist. Die Lösung von
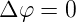 | (3.19) |
ist durch die Randbedingungen
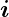 ⊥ = 0 sonst (entlang des Leiters, Drahtoberfläche!)
⊥ = 0 sonst (entlang des Leiters, Drahtoberfläche!)gegeben2 .
Mit diesen Gleichungen kann man zum Beispiel den Widerstand eines homogenen Leiters berechnen. Bei inhomogenen Leitern müssen wir das Ohmsche Gesetz in seiner Differentialform verwenden. Aus der Kontinuitätsgleichung für stationäre Stromverteilungen Gleichung (3.17) und dem lokalen Ohmschen Gesetz Gleichung (3.2) bekommen wir
![div i(x,y,z) = div [σ (x,y,z) E (x,y,z)] = 0](el-2017418x.png) | (3.20) |
Wir ersetzen nun 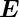 und erhalten
und erhalten
![div [σ(x, y,z)grad U (x,y,z)] = 0](el-2017420x.png) | (3.21) |
Bei einem homogenen Leiter könnte σ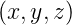 vor die
Divergenz gezogen werden.
vor die
Divergenz gezogen werden.
__________________________________________________________________________
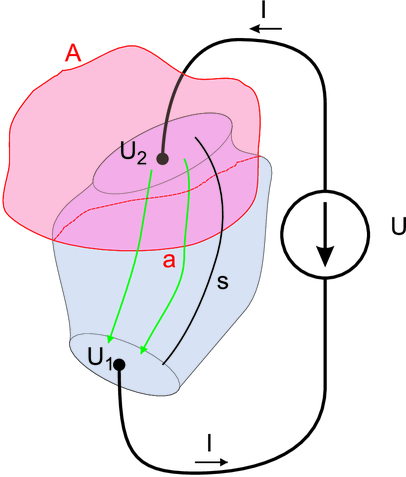
Berechnung des Widerstandes bei einem inhomogenen Leiter
_____________________________________________________________________
Wir verwenden die Definition des Stromes in Gleichung (3.8) und wenden Sie auf die Fläche A, beziehungsweise auf den Teil, der den Leiter durchschneidet a, an.
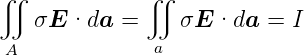 | (3.22) |
wobei a die durch A aus dem Leiter herausgeschnittene Fläche ist. Die Spannungsdifferenz ist
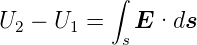 | (3.23) |
Wenn nun φ1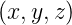 eine Lösung von Gleichung (3.21)
ist, dann ist aufgrund der Linearität dieser Gleichung
auch
eine Lösung von Gleichung (3.21)
ist, dann ist aufgrund der Linearität dieser Gleichung
auch
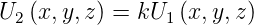 | (3.24) |
eine Lösung. Dabei kann k eine beliebige, auch komplexzahlige
Zahl sein. Da 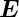 = −grad U auch eine lineare Gleichung ist,
muss also auch
= −grad U auch eine lineare Gleichung ist,
muss also auch
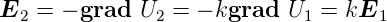 | (3.25) |
eine Lösung sein. Nach Gleichung (3.22) ist dann auch
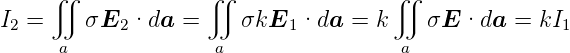 | (3.26) |
Damit haben wir, dass bei einem beliebigen inhomogenen Leiter
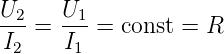 | (3.27) |
ist. Die Proportionalitätskonstante ist der Widerstand
R. Um den Widerstand eines beliebigen Leiters zu
berechnen, muss man 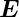
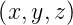 im Inneren kennen. Dies
kann man erreichen, indem man die Laplacegleichung
löst.
im Inneren kennen. Dies
kann man erreichen, indem man die Laplacegleichung
löst.
Im statischen Falle ist  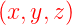 = 0 im Inneren
eines Leiters. Bei einem stromdurchflossenen Leiter
liefert die Batterie die notwendige Energie, um das
elektrische Feld im Inneren des Leiters aufrecht zu
erhalten. = 0 im Inneren
eines Leiters. Bei einem stromdurchflossenen Leiter
liefert die Batterie die notwendige Energie, um das
elektrische Feld im Inneren des Leiters aufrecht zu
erhalten. |
 Lizenzinformationen
Lizenzinformationen