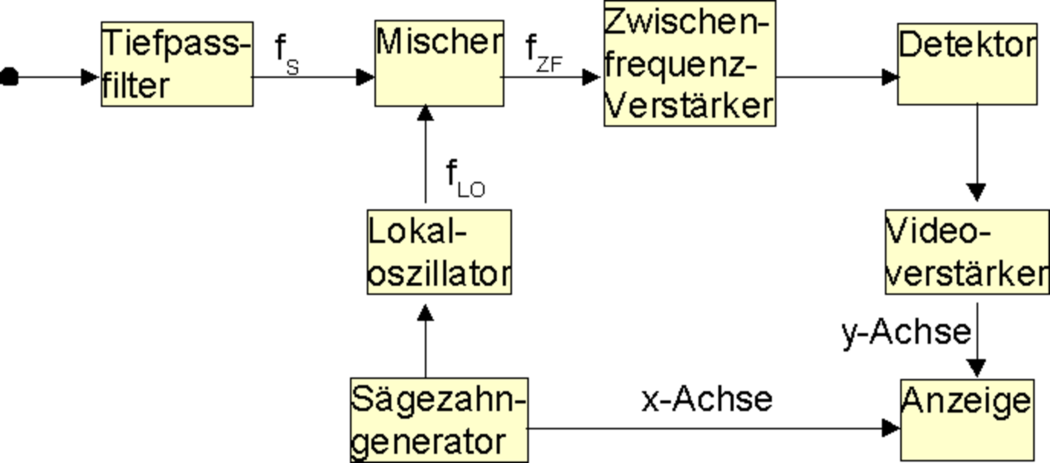
| Abbildung 4.256.: | Blockschaltbild eines Spektralanalysators. |

Bei sehr hohen Frequenzen verwendet man häufig anstelle von Messungen im Zeitbereich Messungen im Frequenzbereich durchgeführt. Bis etwa zu 10 MHz werden Fourieranalysatoren, beruhend auf der schnellen Fouriertransformation (Siehe auch 2.4.2). Für höhere Frequenzen verwendet man Spektralanalysatoren, bei denen die Oszillatoren durchgestimmt werden. Abbildung 4.256 zeigt den Aufbau eines solchen Spektralanalysators. Ein Sägezahnoszillator steuert einen in der Frequenz abstimmbaren Oszillator. Diese Abstimmung könnte zum Beispiel durch einen Schwingkreis mit Kapazitätsdioden realisiert sein. Dieses Signal wird in einem Mischer mit dem tiefpassgefilterten Eingangssignal multipliziert. Aus allen Frequenzen fS des Eingangssignales wird nur derjenige Bereich, der in das Durchlassband des Zwischenfrequenzverstärkers fällt, weiter verstärkt. Dabei ist die Zwischenfrequenz
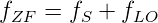 | (4.1) |
Da die Zwischenfrequenz fest ist, wird bei einer Erhöhung der Oszillatorfrequenz die detektierte Signalfrequenz erniedrigt. Wie bei den Lock-In-Verstärkern (siehe auch 4.1.9) legt die Bandbreite des Zwischenfrequenzverstärkers die Bandbreite des Detektionssystems fest. Aus der Filterbandbreite ergibt sich die Messzeit. Die Zeit zur Überstreichung des Frequenzbereiches ist dabei umgekehrt proportional zum Quadrat der Filterbandbreite[BBH98]. Die Quadratische Abhängigkeit kommt von Zwei Faktoren: Einerseits müssen bei einer halben Filterbandbreite doppelt so viele Messpunkte im zu überstreichenden Frequenzbereich. Gleichzeitig ist die Einstellzeit auf eine vorbestimmte Präzision doppelt so lange. Beide Effekte zusammen ergeben eine quadratische Abhängigkeit.
Der Aussteuerungsbereich des Spektrumanalysators wird bei niedrigen Pegeln durch das Geräterauschen und bei hohen Pegeln durch die nichtlinearen Verzerrungen im Mischer begrenzt. Wenn sehr hohe Frequenzen zu messen sind, dann verwendet man Oberwellen des lokalen Oszillators. Bei einer Messung mit der n-ten Oberwelle hängen die gemessene Frequenzkomponente fS und die Zwischenfrequenz fZF wie
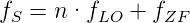 | (4.2) |
zusammen. Es ist damit möglich, bis zu 18 GHz Spektren zu messen. Da die Spiegelfrequenzen schlechter unterdrückt werden, ist die Qualität der Messung nicht so gut wie bei Spektralanalysatoren mit Grundfrequenzoszillatoren.
Neben der Darstellung von modulierten Signalen werden Spektralanalysatoren insbesonders zur Messung von Rauschsignalen (Abschnitt 2.8) verwendet. Bei Zufallsrauschen bedeutet eine Vervierfachung der Bandbreite eine Verdoppelung des Rauschpegels. Man bezieht die Rauschbandbreite eines Spektralanalysators auf die Bandbreite eines Gauss-Filters. Diese ist etwa das 1.2-fache der 3dB-bandbreite[BBH98].
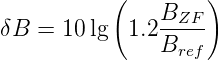 | (4.3) |
Hier ist BZF die Bandbreite des Zwischenfrequenz-Verstärkers. Da in Spektralanalysatoren meistens Spitzenwerte gemessen werden und diese mit einem Faktor passend für eine sinusförmige Schwingung umgerechnet werden, müssen die gemessenen Amplituden bei einer Rauschmessung um 2.5 dB nach oben korrigiert werden.
Bei der Netzwerkanalyse nach Abbildung 4.258 wird ein von einer Quelle stammendes bekanntes Signal an den Eingang eines Netzwerkes gelegt. Das übertragene Signal und das reflektierte Signal werden gemessen.
Beim reflektierten Signal werden
gemessen. Das übertragene Signal wird durch
charakterisiert.
Abbildung 4.258 zeigt den prinzipiellen Aufbau eines Netzwerkanalysators. Die notwendigen Signale werden in einem Signalgenerator erzeugt. Mit diesem Signal wird das zu untersuchende Netzwerk gespiesen. Ein kleiner Bruchteil der ursprünglichen Signalleistung wird in die Schaltung zur Signaltrennung eingespiesen. Dieser Signalanteil dient als Referenz. Das Rückreflektierte Signal wird mit einem Richtkoppler vom Eingangssignal getrennt und in die Signaltrennungsschaltung eingespiesen. Schliesslich wird ein kleiner Bruchteil des übertragenen Signals weiterverarbeitet.
Die Empfänger/Detektorschaltung ist analog zu einem Lock-In-Verstärker aufgebaut und liefert Phase und Amplitude des übertragenen und des reflektierten Signals.
Bei einer Reflexionsmessung wird der Netzwerkanalysator wie in der Abbildung 4.259 gezeigt, verschaltet. Das von einem Signalgenerator kommende Signal wird in einem 6 dB-Teiler in zwei Signale mit je der halben Leistung aufgetrennt. Das eine Signal (oben) dient als Referenz. Das andere wird über einen Richtkoppler[TS80][BBH98] in den Prüfling eingespiesen. Der Richtkoppler trennt das rückreflektierte Signal ab und speist es ebenfalls in den Netzwerkanalysator.
Die Reflexionsmessung kann verwendet werden, wenn man feststellen möchte, ob ein Kabel unterbrochen ist oder ob es einen Kurzschluss hat. In beiden Fällen ist die Impedanz an der Störstelle nicht gleich dem Wellenwiderstand des Kabel: Reflektierte Signale treten auf. Deren Phase zeigt an, ob es sich um einen Kurzschluss oder eine Unterbrechung handelt. Die Laufzeit hängt von der Entfernung der Störstelle ab.

| Abbildung 4.260.: | Detektionsverfahren. a) ist ein Diodendetektor. b) ist ein Grundwellenmischer und c) ein Oberwellenmischer |
Typische Empfängerschaltungen werden in der Abbildung 4.260 gezeigt. Links ist eine einfache Spitzenwertdetektionsschaltung mit einer Diode als Gleichrichter und mit einem Kondensator als Filter angegeben. Damit lässt sich die Einhüllende der detektierten Signale bestimmen. Das mittlere und das rechte Bild zeigen Misch-Verstärker, wie sie auch in Radioempfängerschaltungen eingesetzt werden. Das Eingangssignal wird mit einem um die Zwischenfrequenz versetzten Signal multipliziert und in einem schmalbandigen Filter mit einem festen Durchlassbereich verstärkt und anschliessend demoduliert. Ist die Frequenz des Eingangssignals zu hoch, dann kann der Lokaloszilator einen Hilfsoszillator auf einem Vielfachen seiner Frequenz steuern. Dessen Signal wird mit dem Eingangssignal gemischt. Der verbleibende Teil der Schaltung ist analog zur ursprünglichen Schaltung.
Die Detektion des Zwischenfrequenzsignals kann entweder skalar oder, wie oben angesprochen, über einen Lock-In Verstärker geschehen. Im ersten Falle nennt man das Gerät einen skalaren Netzwerkanalysator, im zweiten Falle handelt es sich um einen vektoriellen Netzwerkanalysator. Abbildung 4.261 zeigt das Funktionsschema eines skalaren Netzwerkanalysators. Das Ausgangssignal eines Signalgenerators wird in einem 6-dB-Teiler auf den Referenzzweig (unten) und den Signalzweig (oben) aufgeteilt. Das Signal wird in einer Zwischenfrequenzstufe (ZF-Filter) entweder direkt nach dem Teiler (Referenzzweig) oder nach Durchlaufen des Prüflings verarbeitet. In beiden Zweigen wird das Signal durch einen Gleichrichter demoduliert. Ein Dividierer bildet den Quotienten aus dem Signal am Ausgang des Prüflings und dem Referenzsignal. Das Resultat wird angezeigt, oder in Rechnern weiterverarbeitet.
Zur Phasenmessung wird der in der Abbildung 4.262 gezeigte Aufbau verwendet. Anstelle eines Dividierers wird ein phasenempfindlicher Detektor verwendet. Die Darstellung von Amplitude und Phase wird vielfach mit einem Smith-Chart durchgeführt. Eine ausführliche Diskussion dieser Darstellungsform findet sich auf der Webseite von Spread Spectrum Scene25 .
Bei einer linearen Übertragungskette ist das Verhältnis zwischen der Ausgangsspannung Uaus und der Eingangsspannung Uein der komplexe Übertragungskoeffizient v. Um eine gültige Übertragungsmessung durchführen zu können, muss der Netzwerkanalysator mit einer bekannten Teststrecke kalibriert werden.
Bei der Untersuchung einer Teststrecke ist von besonderem Interesse, das Verzerrungsverhalten zu bestimmen. Wie man durch Anwendung der Übertragungstheorie (siehe auch den Abschnitt 2.3 und folgende) berechnen kann, ist eine verzerrungsfreie Übertragung nur dann möglich, wenn, wie in Abbildung 4.263 die Amplitude konstant und die Phase linear ist[BBH98]. Der erste Teil dieses Messproblems kann sowohl mit einem skalaren Netzwerkanalysator wie auch mit einem vektoriellen Netzwerkanalysator gelöst werden.
Die Phasenmessung jedoch ist nur mit einem vektoriellen Netzwerkanalysator durchführbar. Um die Wirkung einer linear zunehmenden Phase zu verstehen, betrachten wir die Gruppenlaufzeit
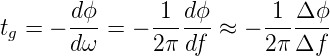 | (4.4) |
Eine linear ansteigende oder abnehmende Phase bedeutet eine konstante Gruppenlaufzeit. Das heisst, dass jede Signalkomponente bei einer Frequenz im Bereich der linearen Phase um die gleiche zeit verzögert wird: Das Signal wird also nicht verzerrt.
Bei einer Messung des Reflexionsverhaltens wird die aus einem Messobjekt in die Quelle zurückreflektierte Spannung UR bestimmt. Sie hängt mit der Eingangsspannung Uein über
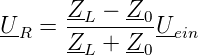 | (4.5) |
zusammen. Z0 ist die (konstante?) Impedanz einer Übertragungsstrecke und ZL ist die Impedanz des Abschlusses der Übertragungsstrecke. Es ist üblich, einen komplexen Reflexionsfaktor
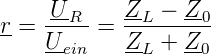 | (4.6) |
zu definieren. Für r gilt, dass 0 ≤|r| = r ≤ 1 ist. Abbildung 4.264 zeigt die Grösse der reflektierten Signale für drei Fälle: Kurzschluss (ZL = 0), Leerlauf (ZL = ∞) und Anpassung (ZL = Z0).
Die rückreflektierte Welle interferiert mit der eingespeisten Welle. Das dabei entstehende Muster von Wellenbergen und Tälern hängt vom Reflexionsfaktor r ab. In der Antennentechnik ist es üblich das Stehwellenverhältnis
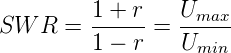 | (4.7) |
zu verwenden. Es gilt, dass 1 ≤SWR ≤∞ ist.
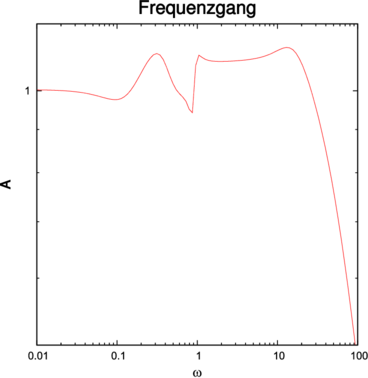

| Abbildung 4.265.: | Links: Frequenzgang des Abschlusswiderstandes für Abbildung 4.266. Rechts ist die entsprechende Nyquist-Darstellung gezeigt. |
Die Transformation des Abschlusswiderstandes (4.6) ist äquivalent zu einer Abbildung der komplexen Ebene auf sich. Wenn alle Impedanzen auf den Wert Z0 bezogen werden, bekommt man für r
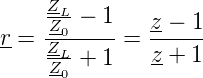 | (4.8) |
Dabei wurde z = ZL∕Z gesetzt. Die Transformation von z nach r ist eine konforme Abbildung auf sich selber. Mit dieser Abbildung nach Gleichung (4.8) kann im Polardiagramm (siehe Abbildung 4.266, links) direkt der Betrag des Reflexionsfaktors und seine Phase abgelesen werden.
Andererseits kann man mit der gleichen Abbildung Gleichung (4.8) auch die Koordinatenachsen und das Gitternetz der Z-Ebene abbilden. Man tranformiert also die Geraden mit konstantem Real- (Widerstands-) und Imaginärteil. Konforme Abbildungen bilden Geraden auf Kreise ab. Die entstehenden Kurven (siehe Abbildung 4.266, rechts) heissen dann Smith-Chart.
Die Transformation der Linien mit konstantem Real- oder Imaginärteil ist im Anhang G.4 gezeigt. Die entstehenden Ortskurven sind Kreise, ihre Anordnung heisst Smith-Chart.
Wir wollen nun einen Abschlusswiderstand, der sich wie in der Abbildung 4.265 verhält, in einen Smith-Chart eintragen. Dazu werden der Real- und der Imaginärteil auf den Gitternetzlinien im Bild 4.266 abgetragen. Die entstehende rote Ortskurve zeigt das reflektierte Signal (abzulesen an den äusseren Achsenbeschriftungen) als Funktion der Abschlussimpedanz.
Polardiagramm und Smith-Chart können kombiniert werden. Dies ist in Abbildung 4.267 gezeigt.
Bei der Berechnung von Schaltungen mit Smith-Charts hilft eine einfache graphische Regel. Nehmen wir an, Z sei die Impedanz und Y ∕Y 0 = Z0∕Z die dazugehörige Admittanz (Dualismus Widerstand - Leitwert). Z0 ist die Referenzimpedanz, Y 0 = 1∕Z0 die Referenzadmittanz. Dann liegt der zu Y ∕Y 0 gehörige Punkt im Smith-Diagramm bei
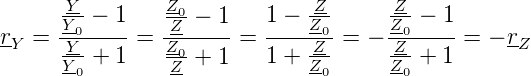
Dies bedeutet, dass die zu Z∕Z0 gehörige Admittanz Y ∕Y 0 einfach am Punkt r = 0 gespiegelt ist. Damit könnenin einem Smith-Chart sehr leicht Reihen- und Parallelschaltungen berechnet werden. Bei Reihenschaltungen von Impedanzen werden die Real- und Imaginärteile addiert. Bei Parallelschaltungen von Impedanzen werden die zugehörigen Admittanzen addiert. Damit kann sehr leicht aus Impedanzkurven im Smith-Chart der resultierende Frequenzverlauf konstruiert werden.
Zur Untersuchung von komplexeren Objekten wie Transistoren oder Verstärkern führt man sie auf Vierpole (siehe auch Abschnitt 2.5) zurück. Im Hoch- und Höchstfrequenzbereich werden bevorzugt die S-Parameter verwendet. Die Definition der S-Parameter ist in der Abbildung 4.268 gezeigt. In Gleichungen gefasst ergibt sich
Die Grössen ai und bi können mit einem vektoriellen Netzwerkanalysator direkt gemessen werden. Durch Messung in Vorwärtsrichtung lassen sich mit a2 = 0
bestimmen. In Rückwärtsrichtung erhält man mit a1 = 0
Damit sind die Kleinsignalparameter eines Prüflings bestimmt.
Bei einem Feldemissionsmikroskop wie auch bei einem Feldionenmikroskop werden Teilchen von einer stark gekrümmten Oberfläche radial emittiert. Die geometrische Situation ist in der Abbildung 4.269 gezeigt. Wenn die Spitze den Krümmungsradius r und der Beobachtungsschirm den Radius R haben, dann ist die Vergrösserung nach dem Strahlensatz durch
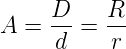 | (4.12) |
Wenn wir für den Beobachtungsschirm einen Radius von R = 0.1m = 10−1m annehmen und für die Spitze einen Krümmungsradius von r = 100nm = 10−7m, dann ist die Vergrösserung A = 106. Zwei Kohlenstoffatome in einem Graphitgitter mit einem Abstand von 0.14nm würden in einem Abstand von 0.14mm abgebildet. Kann der Krümmungsradius der Spitze auf 10nm gesenkt werden, dann würden die zwei Kohlenstoffatome im Abstand von 1.4mm abgebildet.
Bei der Diskussion der Abbildung in einem Feldemissionsmikroskop oder in einem Feldionenmikroskop ist nicht berücksichtigt worden, dass die lokale Topographie den Austrittsort der Elektronen oder den Ort der Feldemission beeinflussen kann. Diese Topographie der Potentiallinien in der Nähe der Spitze mitteln sich jedoch über wenige nm aus, so dass die Trajektorie und damit die Abbildung nicht beeinflusst wird.
Wie in der Abbildung 4.269 diskutiert, bewegen sich die Elektronen auf radialen Trajektorien von der Spitze zum Schirm. Das elektrische Feld in einem Feldemissionsmikroskop entspricht dem eines Kugelkondensators. Die im obigen Abschnitt angesprochene Topographie der Emitterspitze bewirkt eine tangentiale Geschwindigkeit der Elektronen. Diese Tangentialgeschwindigkeit der Elektronen entspricht einer Energie ≈ 0.1 eV. Diese muss mit der gesamten kinetischen Energie von 5 keV verglichen werden, ist also vernachlässigbar.
Die Potentialverhältnisse beim Emissionsprozess von Elektronen werden in der Abbildung 4.270 gezeigt. Die Berechnung kann mit den in den Abschnitten zur Theorie des Tunnelmikroskopes angegebenen Gleichung (??) für den Feldemissionsstrom berechnet werden.
Die Abbildung 4.271 zeigt den prinzipiellen Aufbau eines Feldemissionsmikroskopes. Die Emitterspitze ist in einem Gefäss mit einem Hochvakuum- oder Ultrahochvakuumdruck eingeschlossen. Der Phosphorschirm rechts wandelt die Elektronen entweder direkt oder mit einer vorgeschalteten Mikrokanalplatte in für das Auge sichtbare Bilder um.
Durch die geringe Masse der Elektronen ist deren Brownsche Bewegung so gross, dass eine Abbildung einzelner Atome nicht möglich ist. Deshalb wurde durch Müller und Tsong[ET69] das Feldionenmikroskop entwickelt.
Beim Feldionenmikroskop wird eine positive Spannung an die Spitze angelegt. Ein Abbildungsgas, in der Regel He, H2 oder Ne wird mit niedrigem Druck zur Probenkammer hinzugegeben. Diese ist ähnlich aufgebaut wie die Kammer der Feldemissionsmikroskope (siehe Abbildung 4.271). Die Auflösung bei dieser Art Mikroskopie ist 0.1nm. Sie ist besser als bei der Flemissionsmikroskopie, da die Masse der abbildenden Teilchen sehr viel grösser ist, die Brownsche Bewegung deshalb entsprechend geringer ist.
Die Abbildung 4.273 zeigt den Potentialverlauf an der Spitze eines Feldionenmikroskopes. Wenn ein Atom sich der Oberfläche nähert, verliert es durch Stösse kinetische Energie. Durch die Polarisierbarkeit wird das Atom an der Spitzenoberfläche gehalten. Zwischen dem Atom und der Spitze bildet sich eine Tunnelbarriere. Die Tunnelwahrscheinlichkeit ist desto grösser, je näher das Atom an der Probenoberfläche ist.
Wenn die Austrittsarbeit der Oberfläche ϕ und die Ionisationsenergie I des obersten Energieniveaus ist, dann ist bei einer Feldstärke E an der Spitze die Ionisation durch den Tunneleffekt möglich, wenn
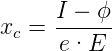 | (4.13) |
Dann liegt das oberste Energieniveau des Atoms über der Fermi-Energie EF . Für Helium liegt das oberste besetzte Niveau , das HeI-Niveau, bei 24.5 eV. Mit der typischen Austrittsarbeit von Wolfram von ϕ = 4.5 eV und einem Feld von 50 V/nm ergibt Gleichung (4.13) für die Ionisationsdistanz den Wert xc = 0.4 nm. Ein Heliumatom aus dem Füllgas der Probenkammer, das durch seine zufällige Bewegung in die Nähe der Spitze kommt, wird durch den Feldgradienten polarisiert. Der entstehende Dipol ist so gerichtet, dass die negative Ladung zur positiven Spitze hin zeigt. Das polarisierte Heliumatom wird deshalb von der positiv geladenen Feldionenmikroskopspitze angezogen und gewinnt an Geschwindigkeit. Wie Bild 4.272 zeigt, stösst das He-Atom mit der Spitze. Durch den teilweise inelastischen Stoss verliert es an Energie. Es wird jedoch, mit verminderter Geschwindigkeit von der Spitze zurückreflektiert. Die Bewegung folgt den Feldlinien des elektrischen Feldes.
Aus der Elektrodynamik ist bekannt, dass sich die Feldlinien des elektrischen Feldes an Orten mit kleinen Krümmungsradien konzentrieren. Dieser Effekt, der auch bei Blitzableitern ausgenutzt wird, bewirkt, dass an Ecken und Kanten die Feldstärke besonders hoch ist. Deshalb sind Ecken und kanten die Orte, Die Feldionisation geschieht bevorzugt an Orten hoher Feldstärke (Ecken, Kanten). Das heisst, dass der nächste und die folgenden Stösse des polarisierten He-Atoms bevorzugt an den Kanten und Ecken geschehen. Nach wenigen Annäherungsbewegungen bleibt das Atom solange an der Oberfläche der Spitze, dass das Valenzelektron (das elektrische Feld bricht die Symmetrie, so dass die Energieniveaux aufspalten) vom Restion getrennt wird. Sobald das He-Atom ionisiert ist, fliegt das Ion entlang der Feldlinien von der Spitze weg und wird auf dem Schirm detektiert.


| Abbildung 4.274.: | Vergleich eines feldionenmikroskopischen Bildes mit einem Kugelmodell. Links ist das Kugelmodell für eine Pt-Kristall gezeigt. Rechts ist das entsprechende feldionenmikroskopische Bild (By Tatsuo Iwata from Sapporo, JAPAN (platinum) [CC BY 2.0 (http://creativecommons.org/licenses/by/2.0)], via Wikimedia Commons. [Iwa17]). |
Abbildung 4.274 zeigt auf der linken Seite ein mit Mathematica gerechnetes Kugelkalottenmodell und ein ein gemessenes Feldionenmikroskopbild [Iwa17].
Damit die Abbildung gelingt, ist es notwendig, dass sowohl die Spitze wie auch die Atome des Füllgases gekühlt werden. Als Kühlmittel werden typischerweise flüssiger Stickstoff (LN2) oder flüssiges Helium (He) verwendet. Damit werden die Tangentialgeschwindigkeiten der He-Ionen klein gehalten.
Die Feldionenmikroskopie war die erste experimentelle Methode, die individuelle Atome abbilden konnte. Da die Spitzen leitfähig sein müssen, ist die Anwendung dieser höchstauflösenden mikroskopischen Methode auf Metalle oder leitfähige Materialien beschränkt.
Erhöht man die an der Spitze angelegte Spannung zu stark, dann ist die Polarisation der Atome an ihrer Oberfläche so gross, dass auch Atome der Spitze im eigenen Feld ionisiert werden. Dieser Effekt wird Felddesorption genannt. Bei erhöhten Feldern wird xc kleiner. Wenn xc in den Bereich von 0.1 nm kommt, werden auch Atome in der Spitzenoberfläche ionisiert.
Spitzen für die Feldionenmikroskopie werden analog zu den Spitzen für die Rastertunnelmikroskopie präpariert (Siehe den Abschnitt ??). Zusätzlich kann der Effekt der Felddesorption zur Formung der Spitze und zur Reduktion der Spitzengrösse verwendet werden. Durch Adsorption aus der Gasphase kann die Spitze auch gezielt vergrössert werden.
Damit ein Material für eine feldionenmikroskopische Abbildung tauglich ist, muss die Felddesorptionsschwelle für die Spitze höher liegen als Feldionisationsschwelle für das Füllgas. Typische in der Feldionenmikroskopie verwendete Materialien sind W, Re, Mo, Fe und Cu. Dazu kommen Mischkristalle und andere, hier nicht genannte Materialien.
Die Abbildung der Geometrie der Probe steht, zumindest bei reinen Oberflächen, heute nicht mehr im Vordergrund. Die Beobachtung der Bewegung einzelner Atome auf Terrassen von 20 bis 30 Substratatomen ermöglicht eine Bestimmung der Sprungwahrscheinlichkeit. Aus dieser lässt sich der Diffusionskoeffizient für einzelne, markierte Atome bestimmen. Wenn der Strom der ionisierten Bildgasatome nicht auf einem Fluoreszenzschirm mit oder ohne vorgeschaltete Mikrokanalplatte, sondern mit einem, die Fläche einer Atomposition abdeckenden Faradaybecher detektiert wird, kann man über die Stromschwankungen auf den Diffusionskoeffizienten rückschliessen.
Die Atom-Probe Feldionenmikroskopie (Abbildung 4.275) ist eine Weiterentwicklung der Feldionenmikroskopie. Die Feldionenmikroskopie erlaubt eine Abbildung der Position von an Kanten oder Ecken sitzenden Atomen. dabei ist jedoch die Atomsorte nicht feststellbar. Die einfachste Art der Atom-Probe-Feldionenmikroskopie beruht darauf, dass bei der Felddesorption ein Atom aus der Probenoberfläche entfernt wird. Die kinetische Energie dieser Ionen hängt von ihrer Masse ab. In einem Massenspektrometer kann, da die Ionen einfach geladen sind, die Masse bestimmt werden.
Wenn die Felddesorption mit Spannungspulsen durchgeführt wird, kann über die Flugzeit der Ionen wie in der Abbildung 4.276 gezeigt die Masse bestimmt werden. Zur Zeit t0 soll ein Spannungspuls an die Spitze angelegt werden. Die Ionen sollen mit der Beschleunigungsspannung U beschleunigt werden. Da die Potentialgradienten des elektrischen Potentials nur in der Nähe der Spitze wesentlich von null verschieden sind, kann man das beschleunigende Feld aus der angelegten Desorptionsspannung berechnen. Zwischen der als konstant angenommenen Geschwindigkeit v, der Masse des Ions mI und der Beschleunigungsspannung gilt die folgende Beziehung.
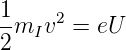 | (4.14) |
Mit der Flugstrecke L, der Distanz zwischen der Spitze und dem Detektor kann die Flugzeit Δt gefunden werden.
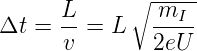 | (4.15) |
Damit ist die Ionenmasse
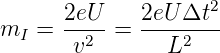 | (4.16) |
Unter der Voraussetzung, dass jedes einzelne Ion detektiert werden kann, kann mit dieser Technik die Oberfläche der Spitze Atom für Atom abgetragen werden. Indem die Spannung des Desorptionspulses so klein gewählt wird, dass im Mittel wesentlich weniger als ein Atom desorbiert wird und indem man nach jedem Desorptionspuls eine Abbildung der Oberfläche aufnimmt, kann man die Zusammensetzung einer Spitze dreidimensional aufgelöst messen.
Wenn man ein Feldemissionsmikroskop als punktförmige Quelle von Elektronen betrachtet kommt man zum Konzept eines Projektionselektronenmikroskopes[FS99]. Es ist möglich, eine Feldemissionsspitze so zu präparieren, dass sie in einem einzelnen Atom endet. Durch dieses einzelne Atom können Ströme von einigen μA fliessen. Durch das kleine Volumen des Atoms, kann sich immer nur ein Elektron in diesem Gebiet aufhalten. Es ist zu erwarten und auch beobachtet worden, dass Elektronen, die aus einem einzelnen Atom emittiert werden, aussergewöhnliche Kohärenzeigenschaften haben.
Abbildung 4.277 zeigt das Prinzip eines Projektionsmikroskopes. Eine feine Spitze wird gegenüber einer Anode mit einem Mikrometer grossen Loch positioniert. Die Spannungsdifferenz zwischen der Spitze und der Anode bestimmt die kinetische Energie der Elektronen. Typischerweise werden Spannungen von einigen 10 Volt angelegt. Dadurch ist die kinetische Energie der Elektronen so gering, dass die Wechselwirkung mit Kohlenstoff zu einem deutlich sichtbaren Kontrast führt[FS99]. Die Vergrösserung eines Projektionselektronenmikroskopes ist durch das Verhältnis der Distanz von der Spitze zum Beobachtungsschirm zur Distanz von der Spitze zum Objekt gegeben.
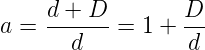 | (4.17) |
Wenn das Objekt einen oder einige Mikrometer von der Spitze entfernt ist und die Distanz zum Schirm 10 cm beträgt, wäre die Vergrösserung zwischen 104 und 105. Die Abbildung mit einem Projektionselektronenmikroskop ist prinzipbedingt verzerrungsfrei und schädigt die Proben kaum.
Abbildung 4.278 zeigt ein simuliertes Hologramm von eine Faserkreuzes. Wenn Interferenzerscheinungen sichtbar sind, deutet dies auf eine für Elektronen aussergewöhnlich hohe Kohärenzlänge hin.
Elektronenbeugung ist eine in der Oberflächenphysik[HG91] übliche Methode zur Untersuchung periodischer Probenoberflächen. In den nächsten beiden Abschnitten werden die Beugung niederenergetischer Elektronen sowie die Beugung von Elektronen mit mittlerer Energie besprochen.
Periodische Anordnungen von Atomen werden Netze genannt. Oberflächennetze sind translationsinvariant. Es gilt also
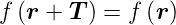 | (4.18) |
mit 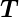 = v
= v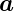 1 + w
1 + w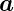 2 wobei
2 wobei 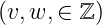 . Dabei ist f die
funktionale Darstellung einer beliebigen Eigenschaft der
Oberfläche. Die Entwicklung von f
. Dabei ist f die
funktionale Darstellung einer beliebigen Eigenschaft der
Oberfläche. Die Entwicklung von f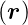 in eine Fourier-Reihe
ergibt
in eine Fourier-Reihe
ergibt
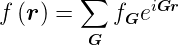 | (4.19) |
Die Summe in Gleichung (4.19) geht über alle reziproken Gittervektoren. Dabei ist
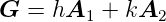 | (4.20) |
wobei h und k ganze Zahlen sind. 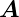 1 und
1 und 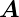 2 sind die
erzeugenden Vektoren des primitiven Netzes.
2 sind die
erzeugenden Vektoren des primitiven Netzes.
Zwischen dem Netz im realen Raum aufgespannt durch 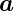 1
und
1
und 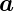 2 und dem Netz im reziproken Raum aufgespannt durch
2 und dem Netz im reziproken Raum aufgespannt durch
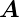 1 und
1 und 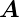 2 muss die Beziehung
2 muss die Beziehung
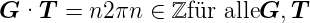 | (4.21) |
Aus den Beziehungen (4.18) bis (4.21) folgt:
Diese Bedingungen werden erfüllt wenn 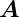 1 und
1 und 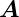 2 wie
folgt konstruiert werden:
2 wie
folgt konstruiert werden:
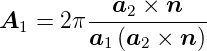 | (4.23) |
und
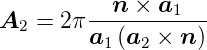 | (4.24) |
Dabei ist 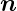 ein beliebiger Vektor senkrecht zum
Oberflächennetz
ein beliebiger Vektor senkrecht zum
Oberflächennetz
Abbildung 4.280 zeigt die Geometrie der Streuung. Die
Einfallende ebene Welle wird mit 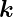 und die gestreute ebene
Welle mit
und die gestreute ebene
Welle mit 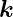 ′ bezeichnet. Der Abstand der Streuzentren sei
′ bezeichnet. Der Abstand der Streuzentren sei
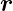 .
.
Die Wegdifferenzen der Wellenzüge zwischen zwei benachbarten Streuzentren sind
Aus dem Wegunterschied berechnet man die Phasendifferenzen zu
Die Phasendifferenz ist
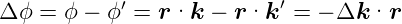 | (4.27) |
mit Δ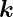 =
= 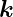 ′−
′−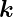 . Für die Amplituden gilt ψ′ = ψeiΔ
. Für die Amplituden gilt ψ′ = ψeiΔ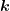 i·
i· für das i-te Atom.
für das i-te Atom.
Für die Beträge der Wellenvektoren gilt
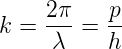 | (4.28) |
mit der de Broglie–Wellenlänge λ und dem Impuls der Teilchen p.
Für die Streuamplitude eines Netzes mit monoatomarer Basis erhält man:
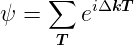 | (4.29) |
mit 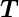 = v·
= v·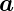 1 + w·
1 + w·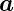 2. Für eine mehratomige Basis erhält
man:
2. Für eine mehratomige Basis erhält
man:
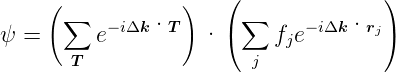 | (4.30) |
fj ist der Streufaktor des j-ten Streuzentrums und 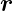 j ist
die Position dieses Streuzentrums in der Einheitszelle.
Der erste Faktor in der Gleichung (4.30) hängt nur vom
Oberflächennetz ab und nicht von der Struktur der
Einheitszelle. Dieser Faktor wird Gittersumme
j ist
die Position dieses Streuzentrums in der Einheitszelle.
Der erste Faktor in der Gleichung (4.30) hängt nur vom
Oberflächennetz ab und nicht von der Struktur der
Einheitszelle. Dieser Faktor wird Gittersumme
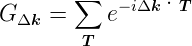 | (4.31) |
genannt. Der zweite Faktor in Gleichung (4.30) ist die geometrische Strukturamplitude
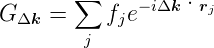 | (4.32) |
Da 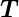 in der Oberfläche liegt, ist
in der Oberfläche liegt, ist
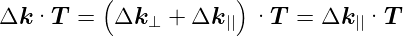 | (4.33) |
Also ist die Laue-Bedingung
Bei elastischer Streuung gilt
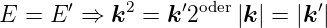 | (4.35) |
Aus dieser Bedingung kann man die in Abb. 4.281 gezeigte Ewald-Konstruktion für Oberflächennetze ableiten.
LEED[ISY82] ist die am häufigsten angewandte Methode zur strukturellen Untersuchung periodischer Kristalloberflächen. Die Elektronen werden mit einer bestimmten, möglichst monochromatischen Energie aus einer wohldefinierten Richtung auf die Probe gesandt. Ihre de Broglie-Wellenlänge muss von der gleichen Grössenordnung wie die Gitterperiode an der Kristalloberfläche sein. Wenn man eine Periodizität von 0.1nm annimmt, so ergibt sich
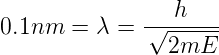 | (4.36) |
Daraus folgt für die Energie
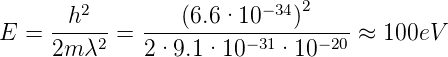 | (4.37) |
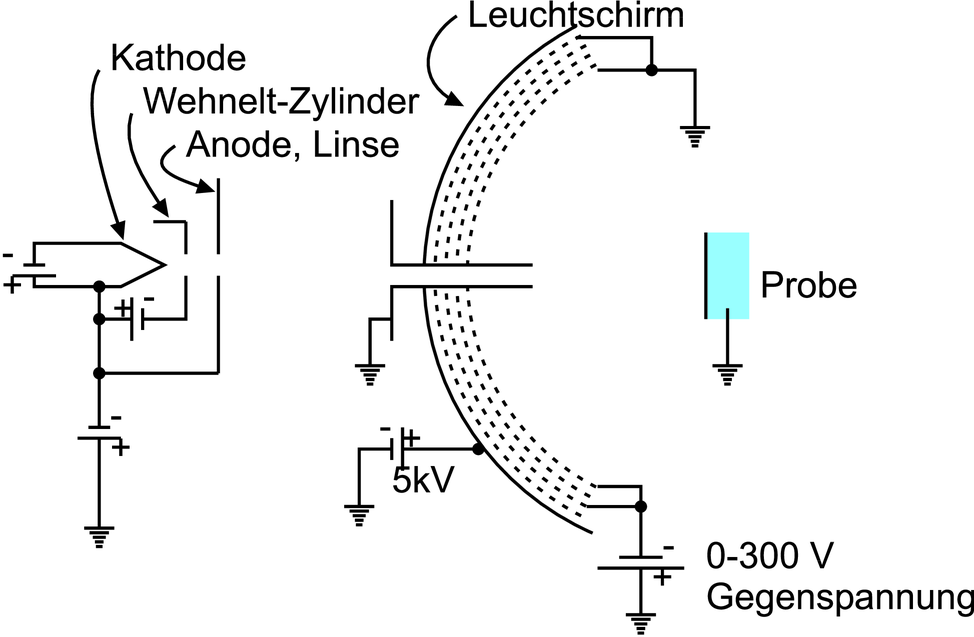
| Abbildung 4.282.: | Aufbau eines LEED. Links ist die Elektronenkanone gezeigt. Rechts ist der schematische Aufbau des LEED-Schirms gezeigt. |
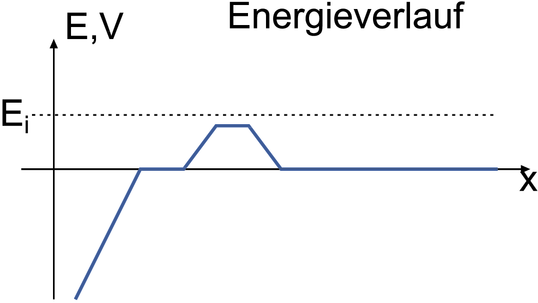
| Abbildung 4.283.: | Energieverlauf im LEED-Detektor. Rechts ist der Zwischenraum zwischen der Probe und dem Detektor. |
Abbildung 4.282 zeigt den Aufbau eines LEED. Die Elektronen stammen in der Regel aus einer thermischen Kathode, wie sie in der Abb. ?? gezeigt ist. Der von den Elektronen bei der Glühemission durchquerte Potentialverlauf ist in der Abb. ?? gezeigt. Nach der Beschleunigungsphase bewegen sich die Elektronen in einem feldfreien Raum bis zur Probe. Die rückgestreuten Elektronen nähern sich dem mit einer phosphoreszierenden Substanz belegten kugelkalottenförmigen Schirm in einem feldfreien Raum. Der Energieverlauf im LEED-Detektor ist schliesslich in der Abb. 4.283 gezeigt.
Die Energieunschärfe bei der Emission muss mit der
thermischen Energie bei Raumtemperatur verglichen werden.
Diese ist ΔE ≈kT ≈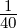 eV . Die Glühemission bei T = 2000K
ist mit einer Energieunschärfe von ΔE ≈ 0.2eV behaftet und
damit etwa acht mal grösser als kT bei Raumtemperatur.
Die Energieunschärfe der Feldemission bei T = 300K
ist schliesslich gleich der thermischen Energie kT, also
ΔE ≈ 0.025eV .
eV . Die Glühemission bei T = 2000K
ist mit einer Energieunschärfe von ΔE ≈ 0.2eV behaftet und
damit etwa acht mal grösser als kT bei Raumtemperatur.
Die Energieunschärfe der Feldemission bei T = 300K
ist schliesslich gleich der thermischen Energie kT, also
ΔE ≈ 0.025eV .
Abbildung 4.284 zeigt die Eindringtiefe der Elektronen als Funktion ihrer kinetischen Energie. Die Eindringtiefe ist für Elektronen mit einer Energie von etwa 100eV minimal. Bei höheren Energien, wie sie zum Beispiel bei RHEED (siehe Abschnitt 4.9.3.4) oder bei der Elektronenmikroskopie (siehe Abschnitt ??) vorkommen ist die Eindringtiefe grösser. Sie nimmt über etwa 500eV monoton mit der kinetischen Energie der Elektronen zu.
Für LEED verwendet man Elektronen mit einer kinetischen Energie von 20 − 500eV . Die Eindringtiefe der Elektronen ist entsprechend kleiner als einen Nanometer.
Das durch die Wechselwirkung der langsamen Elektronen mit der Probe entstehende Beugungsbild kann mit Hilfe der Ewald-Konstruktion nach Abb. 4.285 interpretiert werden.
Zwischen der periodischen Struktur der Probenoberfläche oder einer eventuell vorhandenen Überstruktur und der Überstruktur im reziproken Raum besteht folgender Zusammenhang:
Hier ist nach dem Anhang J S die die Struktur der Oberfläche charakterisierende Matrix. Nach der Gleichung (4.39) kennt man mit Srez auch S.
Damit Beugungseffekte in der Abbildung mit Elektronen beobachtet werden können, muss die Kohärenzlänge der Elektronen grösser als die maximal möglichen Wegunterschiede sein. Wie bei Licht müssen zwei Arten von Kohärenz unterschieden werden.
Mit der Transferweite t (für die Definitionen siehe Abb. 4.286) bezeichnet man die Breite des Elektronenstrahls, die bei perfekter Quelle und perfekter Abbildung die gleiche Breite der Leuchtflächen bewirkt wie der Elektronenstrahl im realen LEED. Sie ist gegeben durch
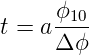 | (4.40) |
Damit wird t ≈ 10nm. Da Elektronen eine sehr kleine Kohärenzlänge haben und da sie als Fermionen nicht im gleichen Quantenzustand sein können26 kann jedes Elektron nur mit sich selber interferieren.

| Abbildung 4.287.: | Schematische Skizze eines LEED-Bildes von Cu(110) (gezeichnet nach [ISY82]). Dies ist eine FCC-Struktur. |

| Abbildung 4.288.: | Schematische Skizze eines LEED-Bildes von Ni (111) bei einer Primärenergie von 205 eV (gezeichnet nach [ISY82]). |
Nicht ideale Oberflächen Bei einer endlich ausgedehnten Probe treten neue Effekte auf. Wir beschreiben die Struktur der Probenoberfläche mit der folgenden Gleichung
 | (4.41) |
Hier sind 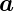 1 und
1 und 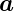 2 die Vektoren, die die Einheitszelle
aufspannen. v und w sind ganze Zahlen, die die einzelnen
Einheitszellen adressieren. Sie können auch als Vektor
2 die Vektoren, die die Einheitszelle
aufspannen. v und w sind ganze Zahlen, die die einzelnen
Einheitszellen adressieren. Sie können auch als Vektor
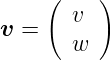 | (4.42) |
geschrieben werden. Die Bewegung der Elektronen wird durch ihren k-Vektor beschrieben.
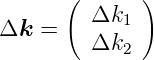 | (4.43) |
Die Wellenfunktion der gestreuten Elektronen ist gegeben durch
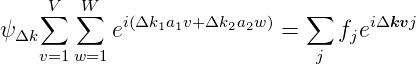 | (4.44) |
Die obigen Gleichungen können für die v- und die w-Komponente einzeln umgeschrieben werden. Man erhält
Diese Summe ist nur ⇔ 0 wenn k1a1 ein Vielfaches von π ist.
Dann ist nach dem Satz von l’Hôspital sin 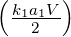 = V . Der
Grenzwert für V →∞ ist die δ–Funktion. Daraus berechnet
sich das Betragsquadrat der Elektronenwellenfunktion
zu
= V . Der
Grenzwert für V →∞ ist die δ–Funktion. Daraus berechnet
sich das Betragsquadrat der Elektronenwellenfunktion
zu
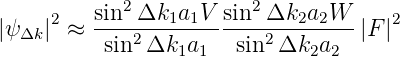 | (4.46) |
wobei |F| der Strukturfaktor aus ∑
jfjeiΔ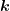
 j ist. Der
Strukturfaktor beinhaltet die Information über die Struktur
der Einheitszelle.
j ist. Der
Strukturfaktor beinhaltet die Information über die Struktur
der Einheitszelle.
Die Breite der Beugungsreflexe ist proportional zu 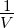 beziehungsweise zu
beziehungsweise zu 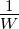 . Diese Aussage folgt aus der Tatsache,
dass die erste Nullstelle von sin(k1a1V ) neben k1a1 = nπ bei
k1a1 −
. Diese Aussage folgt aus der Tatsache,
dass die erste Nullstelle von sin(k1a1V ) neben k1a1 = nπ bei
k1a1 −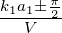 liegt. Deshalb ist die Breite eines Reflexes
liegt. Deshalb ist die Breite eines Reflexes
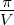 .
.
Domänen Bei vielen asymmetrischen Überstrukturen ist durch das Substrat keine Vorzugsrichtung vorgegeben. Deshalb können Domänen der Überstruktur mit unterschiedlicher Orientierung gleichzeitig auftreten.
Man spricht von einer Mosaikstruktur, wenn gleichzeitig mehrere leicht gegeneinander verkippte Gitter vorliegen.
Paarkorrelation und LEED-Bilder Wir wandeln die Gittersumme in ein Integral um:
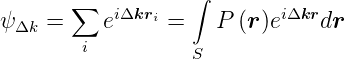 | (4.47) |
mit
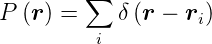 | (4.48) |
also ψΔ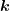 ist die Fouriertransformierte von P
ist die Fouriertransformierte von P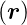
Relationen für Fouriertransformationen:
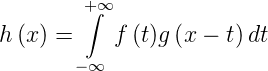 | (4.49) |
und
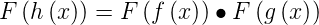 | (4.50) |
einer Faltung entspricht das Produkt der Fouriertransformation.
Wenn wir in der obigen Gleichung g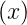 = f∗
= f∗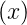 setzen, dann
wird die Autokorrelation
setzen, dann
wird die Autokorrelation
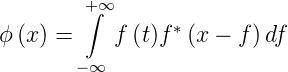 | (4.51) |
Damit wird das Leistungsspektrum
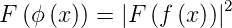 | (4.52) |
Gemessen werden in einem LEED-Experiment oder, allgemeiner, in einem beliebigen Streuexperiment die Intensitäten
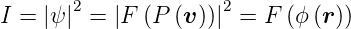 | (4.53) |
Nach der Gleichung (4.53) ist die gemessene Intensität proportional zur Paarkorrelation der Streuzentren. Durch eine Theorie lässt sich aus der Paarkorrelationsfunktion die Intensitätsverteilung berechnen. Die Umkehrung ist aber nicht möglich, da bei der Intensitätsmessung die Phase verloren geht (Phasenproblem).
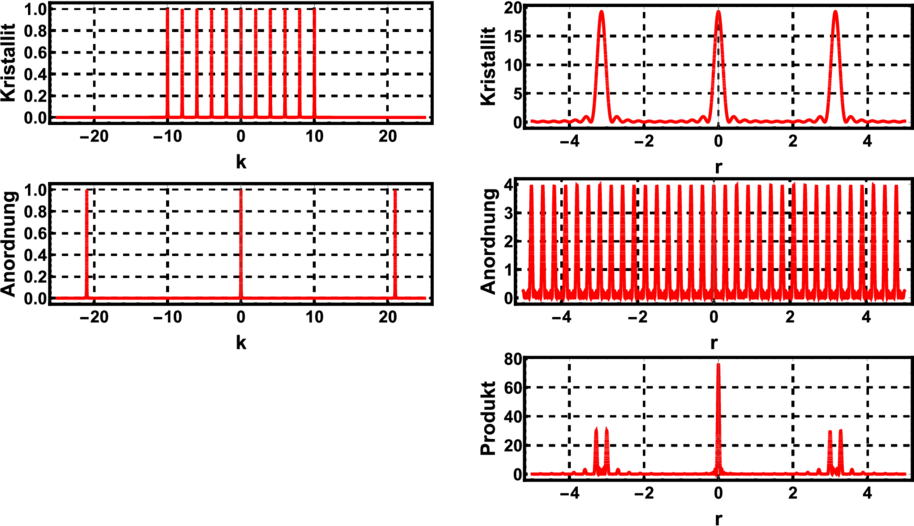
| Abbildung 4.290.: | Beispiel: Regelmässige Domänen einer Kristallstruktur mit der Periode a jeweils im Abstand von (N + 1∕2)a |
Bei einer komplexen Abbildung ist die Fouriertransformation der Paarkorrelationsfunktion der gesamten Abbildung das Produkt der Fouriertransformationen der Paarkorrelationsfunktionen der einzelnen Schritte der Abbildung. Dies entspricht im realen Raum dies einer Faltung. Abbildung 4.290 zeigt als Beispiel die Abbildung mit mehreren Domänen. Dabei ist ersichtlich, dass jeweils jeder zweite Spot ist aufgespalten ist. Sind die Domänen nicht streng periodisch angeordnet, überlagern sich alle möglichen Verbreiterungen. Die LEED-Spots sind dann verbreitert.
Mit dem gleichen Formalismus lassen sich die Beugungsmuster gestufter Oberflächen berechnen.
Gittergase Nichtperiodische Oberflächen können durch Gittergase beschrieben werden. Ein Gittergas ist ein Gas, dessen Teilchen sich statistisch verteilt auf Gitterplätzen aufhalten. Wenn nun eine Welle an dieser statistischen Oberfläche gestreut wird, dann ist die gestreute Intensität
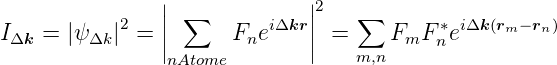 | (4.54) |
Anders als bei periodischen Anordnungen muss jedem Atom eine eigene Streuamplitude angenommen werden. Wenn man statistische Unabhängigkeit annimmt, dann gilt für m ⇔ n
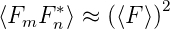 | (4.55) |
da keine Korrelation zwischen den einzelnen Faktoren herrscht. Für den Fall m = n herrscht jedoch eine strenge Korrelation. Deshalb muss zuerst quadriert und dann erst der Mittelwert berechnet werden.
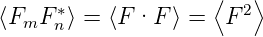 | (4.56) |
Damit wird
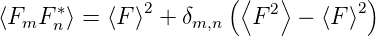 | (4.57) |
Eingesetzt in Gleichung (4.54) erhält man
Aus Gleichung (4.58) ist ersichtlich, dass statistisch verteilte Streuzentren einen konstanten Untergrund bilden. Sie verbreitern die Reflexe jedoch nicht.
Abhängigkeit des LEED-Bildes von der Elektronenenergie
Für Elektronen sind die Intensitäten der Reflexe abhängig von
der Elektronenenergie eV, vom Einfallswinkel φ, von d und von
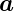 1 und
1 und 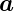 2. Bei der Berechnung der Spannungsabhängigkeit
muss der Einfluss des Strukturfaktors berücksichtigt werden.
Bei einer Änderung der Spannung werden mehr oder weniger
Netzebenen in der Tiefe beteiligt. Immer dann wenn die
Elektronenenergie oder die Beschleunigungsspannung so ist,
dass eine ganze Anzahl Netzebenen berücksichtigt werden,
werden die Strukturfaktoren der beteiligten Atome in allen
Tiefen phasenrichtig addiert. In allen anderen Fällen
mittelt sich die gestreute Amplitude mehr oder weniger
aus.
2. Bei der Berechnung der Spannungsabhängigkeit
muss der Einfluss des Strukturfaktors berücksichtigt werden.
Bei einer Änderung der Spannung werden mehr oder weniger
Netzebenen in der Tiefe beteiligt. Immer dann wenn die
Elektronenenergie oder die Beschleunigungsspannung so ist,
dass eine ganze Anzahl Netzebenen berücksichtigt werden,
werden die Strukturfaktoren der beteiligten Atome in allen
Tiefen phasenrichtig addiert. In allen anderen Fällen
mittelt sich die gestreute Amplitude mehr oder weniger
aus.
Wird die Intensität gegen die Beschleunigungsspannung aufgetragen und nicht gegen den Streuvektor, dann ergeben sich scharfe Maxima für alle Reflexe. Diese Maxima hängen vom Schichtabstand d und, ausser beim 0, 0-Reflex, auch vom Einfallswinkel ab.
Für den 0, 0-Reflex gilt die Bragg-Bedingung für die folgenden Spannungen.
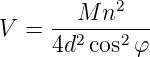 | (4.59) |
mit
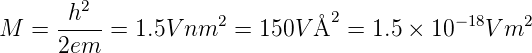 | (4.60) |
Für Vielfache dieser Spannungen treten Intensitätsmaxima
auf. Durch Messung von IΔ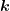
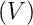 kann die Wechselwirkung
der Elektronen mit der Probe bestimmt werden. Dies wird
auch I-V-Messung genannt.
kann die Wechselwirkung
der Elektronen mit der Probe bestimmt werden. Dies wird
auch I-V-Messung genannt.
Die oben vorgestellte einfache Rechnung kann mit realistischen Potentialen verbessert werden.
Langsame Elektronen werden durch kleine elektrische und magnetische Streufelder abgelenkt. Elektronen höherer Energie zeigen wegen der kürzeren Wechselwirkungszeit mit den Störfeldern weniger Empfindlichkeit. Zudem ist bei höheren Elektronenenergien die relative Energieunschärfe kleiner.
| Abbildung 4.292.: | Geometrie bei der RHEED-Abbildung. Links ist dargestellt, wie die Trajektorien der Elektronen angeordnet sind. Rechts ist gezeigt, wie die Ewald-Konstruktion zum Auffinden der RHEED-Reflexe angewandt werden. |
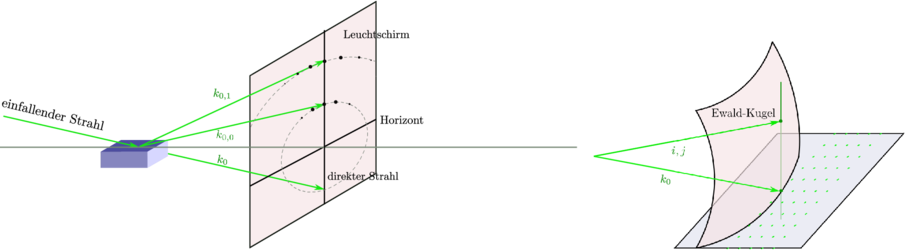
Die Geschwindigkeitskomponente der Elektronen senkrecht zur Oberfläche muss im LEED-Bereich (20-500 eV) sein. Die Energien sind
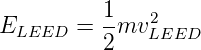 | (4.61) |
und
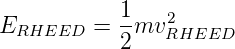 | (4.62) |
Damit kann man die für eine Streuung benötigte Geschwindigkeitskomponente senkrecht zur Probenoberfläche berechnen.
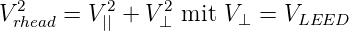 | (4.63) |
Die möglichen Einfallswinkel sind also
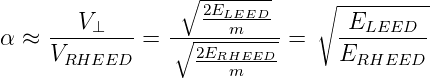 | (4.64) |
Wenn man typische Energien einsetzt wird der Einfallswinkel einer RHEED-Apparatur
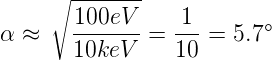 | (4.65) |
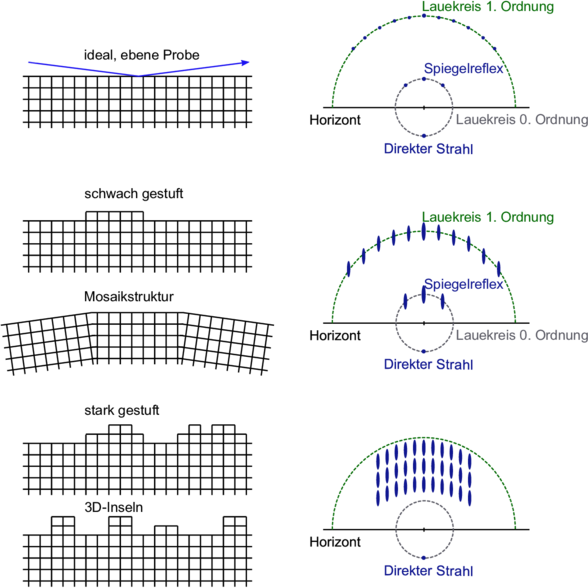
| Abbildung 4.293.: | Konstruktion der Reflexe bei RHEED. Links werden die Strukturen der Oberflächen gezeigt. Rechts ist das entsprechende RHEED-Bild. Von oben nach unten wird die Abbildung bei idealer Oberfläche, bei schwach gestuften Oberflächen, bei einer Mosaikstruktur, stark gestufte Oberflächen sowie 3D-Inseln |
Die bei RHEED Reflexe liegen auf Kreislinien. Bei der RHEED-Abbildung erzeugen Defekte zigarrenförmige Reflexe. Der Spiegelreflex (das ist der 0, 0-Reflex) zeigt Intensitätsmodulationen abhängig von der Oberflächenrauhigkeit.
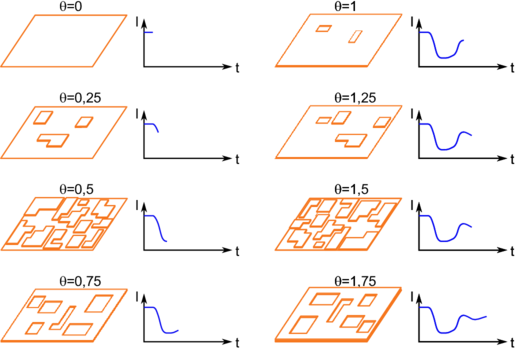
| Abbildung 4.294.: | RHEED-Kontrolle des Schichtwachstums zum Beispiel bei der Herstellung von Halbleiter-Quantenschichten. |
Ein grosser Vorteil der RHEED-Abbildung ist der flache Einfallswinkel der Elektronen. Deshalb ist fast der ganze Halbraum gegenüber der Probenoberfläche frei. Die Probenoberfläche ist für parallele laufende Experimente zugänglich. Typischerweise wird RHEED zur Prozesskontrolle bei Wachstumsprozessen verwendet. Abb. 4.294 zeigt links eine schematische Darstellung der Kristallstruktur und rechts den zeitlichen Verlauf der Intensität des Spiegelreflexes. Die Intensität bei einem perfekten Kristall ist maximal. Wenn das Schichtwachstum startet, dann sinkt die Intensität bis sie bei der halben Bedeckung minimal wird. Wenn eine Monolage voollständig abgeschieden ist, wird wieder ein Maximum erreicht. Dieses ist aber weniger hoch, da mit dem Kristallwachstum immer auch Defekte eingebaut werden.
Im Gegensatz zu LEED ist das reziproke Gitter aus RHEED-Bildern sehr viel schwieriger zu bestimmen.
 Lizenzinformationen
Lizenzinformationen