__________________________________________________________________________
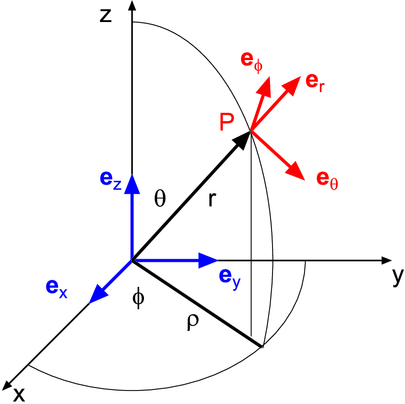
Mitgeführtes orthogonales Koordinatensystem und kartesisches Koordinatensystem
_____________________________________________________________________

Wir betrachten die Definition der Kugelkoordinaten
__________________________________________________________________________

Mitgeführtes orthogonales Koordinatensystem und kartesisches Koordinatensystem
_____________________________________________________________________
Gegeben sind einerseits die kartesischen Koordinaten x, y
und z, andererseits die Kugelkoordinaten r, ϕ, und 𝜃. Am
Punkt P definieren wir ein mitgeführtes kartesisches
Koordinatensystem. Seine Orientierung hängt also von der
Zeit ab! Beide Koordinatensysteme sind jeweils durch ein
Tripel von Einheitsvektoren gegeben, die jeweils gegenseitig
orthogonal sind. Die Einheitsvektoren sind im kartesischen
System 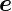 x,
x, 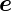 y und
y und 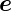 z und im mitgeführten kartesischen
System
z und im mitgeführten kartesischen
System 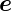 r,
r, 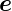 ϕ und
ϕ und 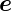 𝜃.
𝜃.
__________________________________________________________________________
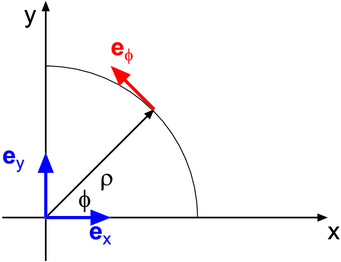
Betrachtung in der xy-Ebene für 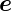 ϕ
ϕ
_______________________________________________________________________________________
Wir betrachten zuerst die xy-Ebene. Die Projektion des Ortsvektors r auf diese Ebene nennen wir ρ. Wir erhalten also die Beziehungen (Einheitsvektoren!)
__________________________________________________________________________
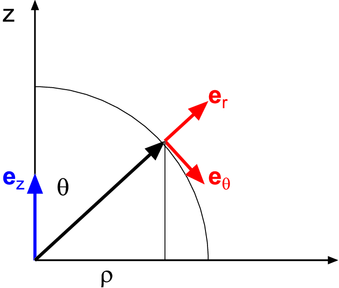
Betrachtung in der ρz-Ebene zur Bestimmung von 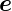 r
und
r
und 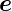 𝜃
𝜃
_______________________________________________________________________________________
Wir betrachten nun die Ebene gebildet aus den Vektoren 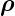 und
und 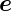 z. In dieser Darstellung ist
z. In dieser Darstellung ist 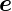 r radial und
r radial und 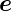 𝜃 zeigt in die
Richtung der positiven 𝜃-Koordinate. Dadurch ist auch
𝜃 zeigt in die
Richtung der positiven 𝜃-Koordinate. Dadurch ist auch 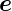 r,
r, 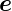 𝜃
und
𝜃
und 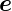 ϕ in dieser Reihenfolge ein ortogonales Rechtssystem.
Aus der Abbildung liest man
ϕ in dieser Reihenfolge ein ortogonales Rechtssystem.
Aus der Abbildung liest man
Dabei merken wir uns, dass 𝜃 und ϕ Funktionen der Zeit sind. Zusammenfassend erhalten wir
Wir wissen, dass 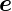 x,
x, 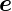 y und
y und 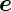 z ein orthogonales Koordinatensystem
ist. Also ist insbesondere 1 =
z ein orthogonales Koordinatensystem
ist. Also ist insbesondere 1 = 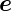 x·
x·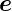 x =
x = 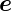 y·
y·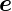 y =
y = 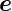 z·
z·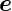 z und
0 =
z und
0 = 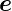 x·
x·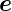 y =
y = 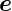 y·
y·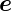 zx =
zx = 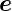 z·
z·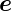 x. Wenn wir mit diesem
Wissen
x. Wenn wir mit diesem
Wissen 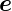 r·
r·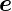 r,
r, 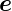 𝜃·
𝜃·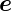 𝜃 und
𝜃 und 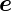 ϕ·
ϕ·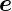 rϕ sowie
rϕ sowie 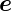 r·
r·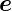 𝜃,
𝜃, 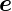 𝜃·
𝜃·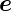 ϕ
und
ϕ
und 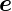 ϕ·
ϕ·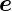 r berechnen, können wir zeigen, dass auch
das Koordinatensystem
r berechnen, können wir zeigen, dass auch
das Koordinatensystem 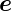 r,
r, 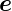 𝜃 und
𝜃 und 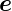 ϕ ein orthogonales
Koordinatensystem ist.
ϕ ein orthogonales
Koordinatensystem ist.
Wenn wir dieses Gleichungssystem nach 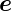 x,
x, 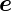 y und
y und 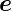 z
auflösen, erhalten wir die Umkehrrelationen
z
auflösen, erhalten wir die Umkehrrelationen
Durch Rückeinsetzen kann man sich überzeugen, dass dies konsistente Formulierungen sind.
 Lizenzinformationen
Lizenzinformationen