


Next: Index
Up: PHYS3100 Physik IIIb
Previous: Satz von Stokes
Die Korrekturen hier sind in dieser aktuellen Version gemacht. Unten stehen die richtigen Gleichungen. Sollten Sie
einen älteren Ausdruck haben, übernehmen Sie bitte die Daten.
- Seite:
![[*]](crossref.gif) , Gleichung (2.66):
, Gleichung (2.66):
-
- Seite:
![[*]](crossref.gif) , Gleichung (2.102):
, Gleichung (2.102):
-
- Seite:
![[*]](crossref.gif) , Gleichung (2.128):
, Gleichung (2.128):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 3.2:
, Abschnitt 3.2:
-
sowie
- Seite:
![[*]](crossref.gif) , Abschnitt 3.2:
, Abschnitt 3.2:
- Die Masse der Ionen sei
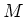 , ihre Ladung
, ihre Ladung 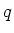 und die Gesamtzahl im betrachteten Volumenelement
und die Gesamtzahl im betrachteten Volumenelement
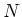
- Seite:
![[*]](crossref.gif) , Abschnitt 3.2:
, Abschnitt 3.2:
- wobei
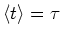 die mittlere Zeit zwischen den
die mittlere Zeit zwischen den
- Seite:
![[*]](crossref.gif) , Gleichung (3.35):
, Gleichung (3.35):
-
- Seite:
![[*]](crossref.gif) , Gleichung (3.36):
, Gleichung (3.36):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 3.1:
, Abschnitt 3.1:
- Mit
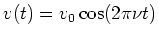 und
und
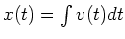 hat man
hat man
Die maximale Strecke erhält man wenn der Sinus von 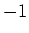 nach
nach 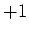 geht.
geht.
Folgerung: bei 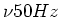 Wechselstrom zittern die Elektronen einige
Wechselstrom zittern die Elektronen einige
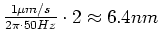 weit.
weit.
- Seite:
![[*]](crossref.gif) , Gleichung (3.37):
, Gleichung (3.37):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 1:
, Abschnitt 1:
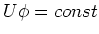 an den Elektrodenflächen
an den Elektrodenflächen
- Seite:
![[*]](crossref.gif) , Abschnitt 3.2:
, Abschnitt 3.2:
- Mit diesen Gleichungen kann man zum Beispiel den Widerstand eines homogenen Leiters berechnen. Bei
inhomogenen Leitern müssen wir das Ohmsche Gesetz in seiner Differentialform verwenden. Aus der
Kontinuitätsgleichung für stationäre Stromverteilungen Gleichung (3.18) und dem lokalen Ohmschen Gesetz
Gleichung (3.26) bekommen wir
- Seite:
![[*]](crossref.gif) , Gleichung (3.47):
, Gleichung (3.47):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 3.7:
, Abschnitt 3.7:
- Die magnetische Induktion
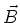 bildet eine Rechtsschraube um den Strom
bildet eine Rechtsschraube um den Strom 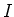 (Daumen in
Stromrichtung, Finger zeigen in die Richtung der magnetischen Induktion).
(Daumen in
Stromrichtung, Finger zeigen in die Richtung der magnetischen Induktion).
- Seite:
![[*]](crossref.gif) , Abschnitt 3.3:
, Abschnitt 3.3:
- Beim van-de-Graaff-Generator besteht diese Arbeit aus zwei Teilen:
- Auf dem Band wird an jedem Punkt die Kraft des elektrostatischen Feldes durch die Kraft des Motors
kompensiert. Auf diesem Zweig ist die Arbeit null.
- Die Arbeit, die im Widerstand in Joulsche
Wärme umgewandelt wird.
- Seite:
![[*]](crossref.gif) , Gleichung (3.87):
, Gleichung (3.87):
-
- Seite:
![[*]](crossref.gif) , Gleichung (3.90):
, Gleichung (3.90):
-
- Seite:
![[*]](crossref.gif) , Gleichung (3.97):
, Gleichung (3.97):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 3.7:
, Abschnitt 3.7:
- Mathematisch kann man
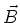 aus einem Linienelement
aus einem Linienelement 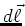 , das parallel zum Leiter und
damit zum Strom ist, und das in die Flussrichtung des Stromes zeigt und aus dem Vektor
, das parallel zum Leiter und
damit zum Strom ist, und das in die Flussrichtung des Stromes zeigt und aus dem Vektor 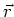 , der vom
Leiterelement zum Ort, an dem das Magnetfeld betrachtet werden sollte, zeigt, berechnen
, der vom
Leiterelement zum Ort, an dem das Magnetfeld betrachtet werden sollte, zeigt, berechnen
- Seite:
![[*]](crossref.gif) , Gleichung (3.116):
, Gleichung (3.116):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 3.7.1:
, Abschnitt 3.7.1:
- Wir betrachten viele Ströme
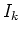 , die
von der Integrationskurve
, die
von der Integrationskurve 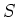 umschlossen werden. Wegen der Linearität des Problems gilt
umschlossen werden. Wegen der Linearität des Problems gilt
wobei diejenigen Ströme, die mit dem Umlaufsinn von 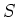 eine Rechtsschraube bilden, positiv zu zählen sind.
eine Rechtsschraube bilden, positiv zu zählen sind.
- Seite:
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2:
- Da überall auf der Integrationsfläche
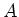 gilt:
gilt:
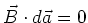 , ist
, ist
- Seite:
![[*]](crossref.gif) , Gleichung (3.130):
, Gleichung (3.130):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2:
-
- Seite:
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2:
-
- Seite:
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2:
-
- Seite:
![[*]](crossref.gif) , Gleichung (3.131):
, Gleichung (3.131):
-
- Seite:
![[*]](crossref.gif) , Gleichung (3.132):
, Gleichung (3.132):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 3.7.3:
, Abschnitt 3.7.3:
- Wenn wir mit
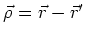 den Abstand von einem Beobachtungspunkt
den Abstand von einem Beobachtungspunkt 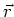 zu
einem Punkt
zu
einem Punkt 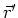 mit der Stromdichte
mit der Stromdichte
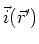 eines linearen Leiterstückes
eines linearen Leiterstückes
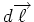 bezeichnen und
bezeichnen und
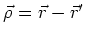 setzen, ist der Beitrag zum magnetischen Feld
setzen, ist der Beitrag zum magnetischen Feld
- Seite:
![[*]](crossref.gif) , Gleichung (3.139):
, Gleichung (3.139):
-
- Seite:
![[*]](crossref.gif) , Gleichung (3.165):
, Gleichung (3.165):
-
- Seite:
![[*]](crossref.gif) , Gleichung (4.1):
, Gleichung (4.1):
-
- Seite:
![[*]](crossref.gif) , Gleichung (4.46):
, Gleichung (4.46):
-
- Seite:
![[*]](crossref.gif) , Gleichung (4.49):
, Gleichung (4.49):
-
- Seite:
![[*]](crossref.gif) , Gleichung (4.50):
, Gleichung (4.50):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 4.1.7:
, Abschnitt 4.1.7:
- Der Mittelwert der Leistung ist (
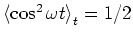 )
)
- Seite:
![[*]](crossref.gif) , Gleichung (4.67):
, Gleichung (4.67):
-
- Seite:
![[*]](crossref.gif) , Gleichung (4.68):
, Gleichung (4.68):
-
- Seite:
![[*]](crossref.gif) , Gleichung (4.93):
, Gleichung (4.93):
-
- Seite:
![[*]](crossref.gif) , Gleichung (4.95):
, Gleichung (4.95):
-
- Seite:
![[*]](crossref.gif) , Gleichung (4.137):
, Gleichung (4.137):
-
- Seite:
![[*]](crossref.gif) , Gleichung (5.8):
, Gleichung (5.8):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 4.3.5:
, Abschnitt 4.3.5:
- oder mit
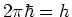
- Seite:
![[*]](crossref.gif) , Gleichung (5.2):
, Gleichung (5.2):
-
- Seite:
![[*]](crossref.gif) , Gleichung (5.11):
, Gleichung (5.11):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 5:
, Abschnitt 5:
- Der Unterschied zwischen der zweiten und der dritten Maxwellgleichung ist, dass in der zweiten Gleichung über eine
einfache, von der Kurve
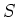 aufgespannte Fläche
aufgespannte Fläche 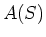 integriert wird, während in der dritten Gleichung über die
das Volumen
integriert wird, während in der dritten Gleichung über die
das Volumen 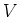 einschliessende Fläche
einschliessende Fläche 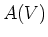 integriert wird.
integriert wird.
- Seite:
![[*]](crossref.gif) , Gleichung (5.13):
, Gleichung (5.13):
-
- Seite:
![[*]](crossref.gif) , Gleichung (5.14):
, Gleichung (5.14):
-
- Seite:
![[*]](crossref.gif) , Gleichung (5.16):
, Gleichung (5.16):
-
- Seite:
![[*]](crossref.gif) , Gleichung (5.19):
, Gleichung (5.19):
-
- Seite:
![[*]](crossref.gif) , Gleichung (6.1):
, Gleichung (6.1):
-
- Seite:
![[*]](crossref.gif) , Gleichung (6.2):
, Gleichung (6.2):
-
- Seite:
![[*]](crossref.gif) , Abschnitt 6.1:
, Abschnitt 6.1:
- Im Vakuum ist
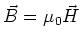 sowie
sowie
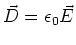 sowie
sowie 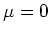 und
und 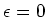 .
.
- Seite:
![[*]](crossref.gif) , Gleichung (6.7):
, Gleichung (6.7):
-
- Seite:
![[*]](crossref.gif) , Gleichung (6.8):
, Gleichung (6.8):
-
- Seite:
![[*]](crossref.gif) , Gleichung (6.11):
, Gleichung (6.11):
-
- Seite:
![[*]](crossref.gif) , Gleichung (6.22):
, Gleichung (6.22):
-
- Seite:
![[*]](crossref.gif) , Gleichung (6.25):
, Gleichung (6.25):
-
- Seite:
![[*]](crossref.gif) , Gleichung (6.26):
, Gleichung (6.26):
-
- Seite:
![[*]](crossref.gif) , Gleichung (6.30):
, Gleichung (6.30):
-
- Seite:
![[*]](crossref.gif) , Gleichung (6.49):
, Gleichung (6.49):
-




Next: Index
Up: PHYS3100 Physik IIIb
Previous: Satz von Stokes
Othmar Marti
Experimentelle Physik
Universiät Ulm
![[*]](crossref.gif) , Gleichung (2.66):
, Gleichung (2.66):![[*]](crossref.gif) , Gleichung (2.102):
, Gleichung (2.102):![[*]](crossref.gif) , Gleichung (2.128):
, Gleichung (2.128):![[*]](crossref.gif) , Abschnitt 3.2:
, Abschnitt 3.2:![[*]](crossref.gif) , Abschnitt 3.2:
, Abschnitt 3.2:![[*]](crossref.gif) , Abschnitt 3.2:
, Abschnitt 3.2:![[*]](crossref.gif) , Gleichung (3.35):
, Gleichung (3.35):![[*]](crossref.gif) , Gleichung (3.36):
, Gleichung (3.36):![[*]](crossref.gif) , Abschnitt 3.1:
, Abschnitt 3.1:![]() nach
nach ![]() geht.
geht.
![]() Wechselstrom zittern die Elektronen einige
Wechselstrom zittern die Elektronen einige
![]() weit.
weit.
![[*]](crossref.gif) , Gleichung (3.37):
, Gleichung (3.37):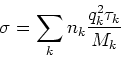
![[*]](crossref.gif) , Abschnitt 1:
, Abschnitt 1:![[*]](crossref.gif) , Abschnitt 3.2:
, Abschnitt 3.2:![[*]](crossref.gif) , Gleichung (3.47):
, Gleichung (3.47):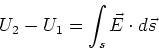
![[*]](crossref.gif) , Abschnitt 3.7:
, Abschnitt 3.7:![[*]](crossref.gif) , Abschnitt 3.3:
, Abschnitt 3.3:![[*]](crossref.gif) , Gleichung (3.87):
, Gleichung (3.87):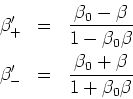
![[*]](crossref.gif) , Gleichung (3.90):
, Gleichung (3.90):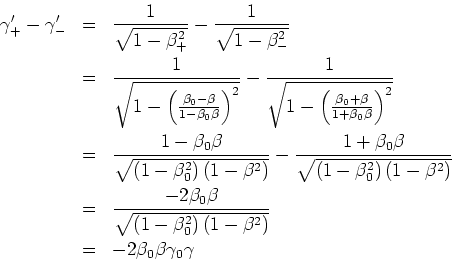
![[*]](crossref.gif) , Gleichung (3.97):
, Gleichung (3.97):![[*]](crossref.gif) , Abschnitt 3.7:
, Abschnitt 3.7: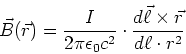
![[*]](crossref.gif) , Gleichung (3.116):
, Gleichung (3.116):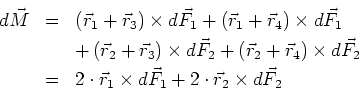
![[*]](crossref.gif) , Abschnitt 3.7.1:
, Abschnitt 3.7.1: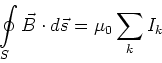
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2:![[*]](crossref.gif) , Gleichung (3.130):
, Gleichung (3.130):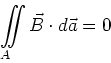
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2: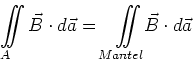
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2: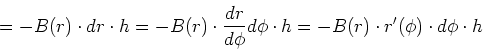
![[*]](crossref.gif) , Abschnitt 3.7.2:
, Abschnitt 3.7.2: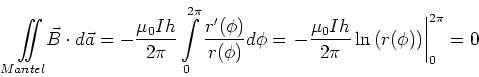
![[*]](crossref.gif) , Gleichung (3.131):
, Gleichung (3.131):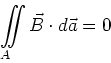
![[*]](crossref.gif) , Gleichung (3.132):
, Gleichung (3.132):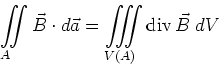
![[*]](crossref.gif) , Abschnitt 3.7.3:
, Abschnitt 3.7.3:![[*]](crossref.gif) , Gleichung (3.139):
, Gleichung (3.139):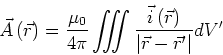
![[*]](crossref.gif) , Gleichung (3.165):
, Gleichung (3.165):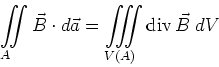
![[*]](crossref.gif) , Gleichung (4.1):
, Gleichung (4.1):![[*]](crossref.gif) , Gleichung (4.46):
, Gleichung (4.46):![[*]](crossref.gif) , Gleichung (4.49):
, Gleichung (4.49):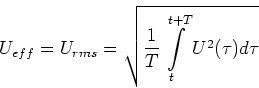
![[*]](crossref.gif) , Gleichung (4.50):
, Gleichung (4.50):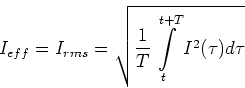
![[*]](crossref.gif) , Abschnitt 4.1.7:
, Abschnitt 4.1.7:![[*]](crossref.gif) , Gleichung (4.67):
, Gleichung (4.67):![[*]](crossref.gif) , Gleichung (4.68):
, Gleichung (4.68):![[*]](crossref.gif) , Gleichung (4.93):
, Gleichung (4.93):
![[*]](crossref.gif) , Gleichung (4.95):
, Gleichung (4.95):![[*]](crossref.gif) , Gleichung (4.137):
, Gleichung (4.137):![[*]](crossref.gif) , Gleichung (5.8):
, Gleichung (5.8):
![[*]](crossref.gif) , Abschnitt 4.3.5:
, Abschnitt 4.3.5:![[*]](crossref.gif) , Gleichung (5.2):
, Gleichung (5.2):![[*]](crossref.gif) , Gleichung (5.11):
, Gleichung (5.11):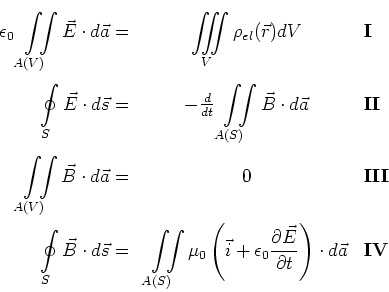
![[*]](crossref.gif) , Abschnitt 5:
, Abschnitt 5:![[*]](crossref.gif) , Gleichung (5.13):
, Gleichung (5.13):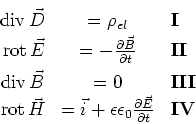
![[*]](crossref.gif) , Gleichung (5.14):
, Gleichung (5.14):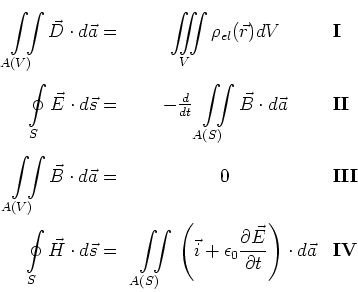
![[*]](crossref.gif) , Gleichung (5.16):
, Gleichung (5.16):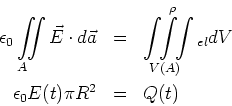
![[*]](crossref.gif) , Gleichung (5.19):
, Gleichung (5.19):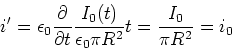
![[*]](crossref.gif) , Gleichung (6.1):
, Gleichung (6.1):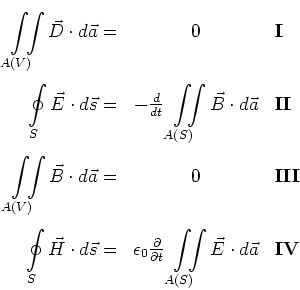
![[*]](crossref.gif) , Gleichung (6.2):
, Gleichung (6.2):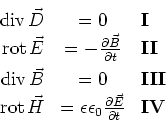
![[*]](crossref.gif) , Abschnitt 6.1:
, Abschnitt 6.1:![[*]](crossref.gif) , Gleichung (6.7):
, Gleichung (6.7):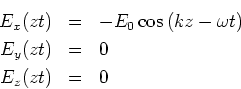
![[*]](crossref.gif) , Gleichung (6.8):
, Gleichung (6.8):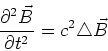
![[*]](crossref.gif) , Gleichung (6.11):
, Gleichung (6.11):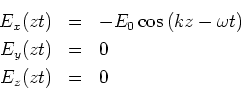
![[*]](crossref.gif) , Gleichung (6.22):
, Gleichung (6.22):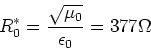
![[*]](crossref.gif) , Gleichung (6.25):
, Gleichung (6.25):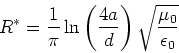
![[*]](crossref.gif) , Gleichung (6.26):
, Gleichung (6.26):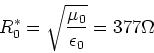
![[*]](crossref.gif) , Gleichung (6.30):
, Gleichung (6.30):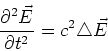
![[*]](crossref.gif) , Gleichung (6.49):
, Gleichung (6.49):